
【题目】已知二次函数的图象经过点A(1,2)和B(0,-1)且对称轴为x2.
(1)求这个二次函数的解析式;
(2)抛物线上点P(2,m)在图象上,求△PAB的面积.
科目:初中数学 来源: 题型:
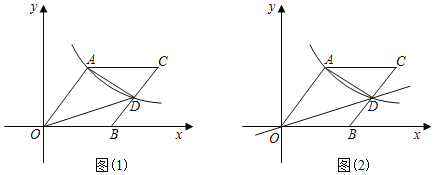
【题目】如图(1),![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴的正半轴上,四边形
轴的正半轴上,四边形![]() 是平行四边形,
是平行四边形,![]() ,
,![]() ,反比例函数
,反比例函数![]() 在第一象限内的图象经过点
在第一象限内的图象经过点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求点![]() 的坐标和反比例函数解析式;
的坐标和反比例函数解析式;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)在(2)中的条件下,如图(2),点![]() 为直线
为直线![]() 上的一个动点,点
上的一个动点,点![]() 为双曲线上的一个动点,是否在这样的点
为双曲线上的一个动点,是否在这样的点![]() 、点
、点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形?若存在,请直接写出所有点
为顶点的四边形是平行四边形?若存在,请直接写出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
与x轴交于A、B两点,与y轴交于点C,点D与点C关于x轴对称,点P从A点出发向点D运动,点Q在DB上,且∠PCQ=45°,则封闭图形DPCQ(阴影部分)面积的变化情况是( )
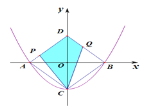
A.一直变大B.始终不变C.先增大后减少D.先减少后增大
查看答案和解析>>
科目:初中数学 来源: 题型:
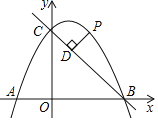
【题目】如图,直线y=﹣x+4与x轴,y轴分别交于点B,C,点A在x轴负半轴上,且OA=![]() OB,抛物线y=ax2+bx+4经过A,B,C三点.
OB,抛物线y=ax2+bx+4经过A,B,C三点.
(1)求抛物线的解析式;
(2)点P是第一象限内抛物线上的动点,设点P的横坐标为m,过点P作PD⊥BC,垂足为D,用含m的代数式表示线段PD的长,并求出线段PD的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=8,AD=17,折叠纸片使点B落在边AD上的E处,折痕为PQ.当E在AD边上移动时,折痕的端点P,Q也随着移动.若限定P,Q分别在边BA,BC上移动,则点E在边AD上移动的最大距离为( )
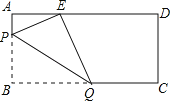
A.6B.7C.8D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宏兴企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系: ![]() .
.
(1)工人甲第几天生产的产品数量为70件?
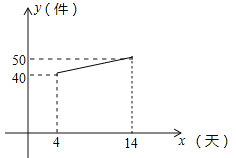
(2)设第x天生产的产品成本为P元/件,P与x的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时,利润最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,为激发同学们的学习热情,王华所在的学校组织全校三好学生分别到A,B,C,D四所全国重点学校参观(每个学生只能去一处),王华很高兴她也能够前往,学校按定额购买了前往四地的车票.如图是未制作完成的车票种类和数量的条形统计图和扇形统计图.请根据以上信息回答:

(1)本次参加参观的学生有 人,将条形统计图补充完整;
(2)若学校采用随机抽取的方式分发车票,每人一张(所有车票的形状、大小、质地完全相同且充分洗匀),那么王华抽到去B地的概率是多少?
(3)已知A,B,C三地车票的价格如下表,去D地花费的车票总款数占全部车票总款数的![]() ,试求D地每张车票的价格.
,试求D地每张车票的价格.
地点 | 票价(元/张) |
A | 60 |
B | 80 |
C | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com