
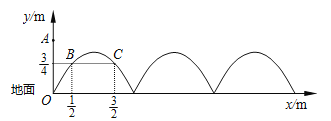
【题目】如图,需在一面墙上绘制几个相同的抛物线型图案.按照图中的直角坐标系,最左边的抛物线可以用![]() (a≠0)表示.已知抛物线上B,C两点到地面的距离均为
(a≠0)表示.已知抛物线上B,C两点到地面的距离均为![]() m,到墙边OA的距离分别为
m,到墙边OA的距离分别为![]() m,
m,![]() m.
m.
(1)求该拋物线的函数关系式,并求图案最高点到地面的距离;
(2)若该墙的长度为10m,则最多可以连续绘制几个这样的拋物线型图案?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图1,在□ABCD中,AE⊥BC于E,E恰为BC的中点,tanB=2。



(1)求证:AD=AE;
(2)如图2,点P在BE上,作EF⊥DP于点F,连结AF,求证:DF-EF=![]() AF;
AF;
(3)请你在图3中画图探究:当P为射线EC上任意一点(P不与点E重合)时,作EF⊥DP于点F,连结AF,线段DF、EF与AF之间有怎样的数量关系?直接写出你的结论为____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在长和宽分别是 ![]() 、
、 ![]() 的矩形纸片的四个角上都剪去一个边长为
的矩形纸片的四个角上都剪去一个边长为 ![]() 的小正方形,折成一个无盖的纸盒.
的小正方形,折成一个无盖的纸盒.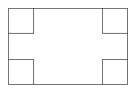
(1)用a , b , x表示纸片剩余部分的面积;
(2)当a=16,b=12,且剪去部分的面积等于剩余部分的面积的一半时,求小正方形的边长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CE=2DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FGC=3.6.其中正确结论的个数是( )
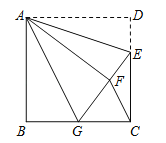
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且B点和C点在AE的异侧,BD⊥AE于D点,CE⊥AE与E点.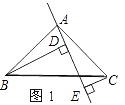
(1)求证:BD=DE+CE
(2)若直线AE绕点A旋转到图2所示的位置时(BD<CE)其余条件不变,问BD 与DE,CE的关系如何?请予以证明.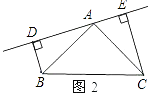
(3)若直线AE绕点A旋转到图3所示的位置时(BD>CE)其余条件不变,问BD 与DE,CE的关系如何?直接写出结果,不需证明.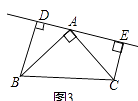
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: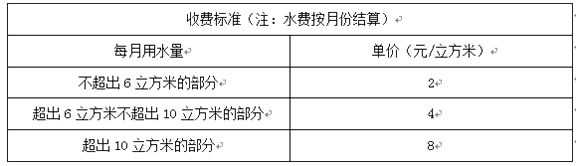
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费元;
(2)若某户居民3月份交水费36元,则用水量为立方米;
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费元.
(4)若某户居民 5、6 两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该居民5、6两个月共交水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com