
分析 (1)把x=20代入y=-10x+500求出销售的件数,然后求出政府承担的成本价与出厂价之间的差价;
(2)由总利润=销售量•每件纯赚利润,得w=(x-10)(-10x+500),把函数转化成顶点坐标式,根据二次函数的性质求出最大利润;
(3)令-10x2+600x-5000=3000,求出x的值,结合图象求出利润的范围,然后设政府每个月为他承担的总差价为p元,根据一次函数的性质求出总差价的最小值.
解答 解:(1)当x=20时,y=-10x+500=-10×20+500=300,
300×(12-10)=300×2=600元,
即政府这个月为他承担的总差价为600元.
(2)由题意得,w=(x-10)(-10x+500)
=-10x2+600x-5000
=-10(x-30)2+4000
∵a=-10<0,
∴当x=30时,w有最大值4000元.
即当销售单价定为30元时,每月可获得最大利润4000元.
(3)由题意得:-10x2+600x-5000=3000,
解得:x1=20,x2=40.
∵a=-10<0,抛物线开口向下,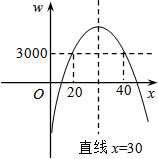
∴结合图象可知:当20≤x≤40时,4000>w≥3000.
又∵x≤25,
∴当20≤x≤25时,w≥3000.
设政府每个月为他承担的总差价为p元,
∴p=(12-10)×(-10x+500)
=-20x+1000.
∵k=-20<0.
∴p随x的增大而减小,
∴当x=25时,p有最小值500元.
即销售单价定为25元时,政府每个月为他承担的总差价最少为500元.
点评 本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解,此题难度不大.


科目:初中数学 来源: 题型:解答题
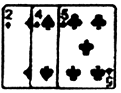 三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.
三张扑克牌的牌面如图所示,这三张扑克牌除牌面不同外,其它均相同.将这三张扑克牌背面朝上洗匀,从中随机抽出一张,记下数字后放回;重新洗匀后从中再随机抽出一张,记下数字.请用画树状图(或列表)的方法,求抽出的两张扑克牌上的数字之和是9的概率.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:| 种类 | 频数 | 百分比 |
| A.科普类 | 12 | 30% |
| B.文学类 | n | 35% |
| C.艺术类 | m | 20% |
| D.其它类 | 6 | 15% |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是(1,1),△ABC的面积为4.
在8×8的正方形网格中建立如图所示的平面直角坐标系,已知A(2,4),B(4,2).C是第一象限内的一个格点,由点C与线段AB组成一个以AB为底,且腰长为无理数的等腰三角形.C点的坐标是(1,1),△ABC的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com