
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬AC=BC£¬Ö±ĻßMN¾¹żµćC£¬ĒŅAD”ĶMNÓŚD£¬BE”ĶMNÓŚE£®
£Ø1£©µ±Ö±ĻßMNČʵćCŠż×Ŗµ½¢ŁµÄĪ»ÖĆŹ±£¬ĒóÖ¤£ŗ¢Ł”÷ADC”Õ”÷CEB£»¢ŚDE=AD+BE£»
£Ø2£©µ±Ö±ĻßMNČʵćCŠż×Ŗµ½¢ŚµÄĪ»ÖĆŹ±£¬ĒóÖ¤£ŗDE=AD©BE£»
£Ø3£©µ±Ö±ĻßMNČʵćCŠż×Ŗµ½¢ŪµÄĪ»ÖĆŹ±£¬ŹŌĪŹDE”¢AD”¢BE¾ßÓŠŌõŃłµÄŹżĮæ¹ŲĻµ£æĒėÖ±½ÓŠ“³öÕāøöµČĮæ¹ŲĻµ£¬²»ŠčŅŖÖ¤Ć÷£®

”¾“š°ø”æ£Ø1£©¢ŁÖ¤Ć÷¼ū½āĪö¢ŚDE=CE+CD=AD+BE£Ø2£©Ö¤Ć÷¼ū½āĪö£Ø3£©DE=BE©AD£Ø»ņAD=BE©DE£¬BE=AD+DEµČ£©
”¾½āĪö”æ
(1£©ÓÉ”ĻACB=90”ć£¬µĆ”ĻACD+”ĻBCE=90”ć£¬¶ųAD”ĶMNÓŚD£¬BE”ĶMNÓŚE£¬Ōņ”ĻADC=”ĻCEB=90”ć£¬øł¾ŻµČ½ĒµÄÓą½ĒĻąµČµĆµ½”ĻACD=”ĻCBE£¬Ņ׵Ɣ÷ADC”Õ”÷CEB£¬
ÓÉ”÷ADC”Õ”÷CEBĖłŅŌAD=CE£¬DC=BE£¬¼“æɵƵ½DE=DC+CE= AD+ BE£®
£Ø2£©ÓÉ”ĻACB=90”ć£¬µĆ”ĻACD+”ĻBCE=90”ć£¬¶ųAD”ĶMNÓŚD£¬BE”ĶMNÓŚE£¬Ōņ”ĻADC=”ĻCEB=90”ć£¬øł¾ŻµČ½ĒµÄÓą½ĒĻąµČµĆµ½”ĻACD=”ĻCBE£¬Ņ׵Ɣ÷ADC”Õ”÷CEB£¬
ÓÉ”÷ADC”Õ”÷CEBĖłŅŌAD=CE£¬DC=BE¼“æɵƵ½DE =CE-CD=AD©BE
(3) ÓÉ”ĻACB=90”ć£¬µĆ”ĻACD+”ĻBCE=90”ć£¬¶ųAD”ĶMNÓŚD£¬BE”ĶMNÓŚE£¬Ōņ”ĻADC=”ĻCEB=90”ć£¬øł¾ŻµČ½ĒµÄÓą½ĒĻąµČµĆµ½”ĻACD=”ĻCBE£¬Ņ׵Ɣ÷ADC”Õ”÷CEB£¬
ÓÉ”÷ADC”Õ”÷CEBĖłŅŌAD=CE£¬DC=BE¼“æɵƵ½DE =CD-CE=BE©AD£®
£Ø1£©¢ŁÖ¤Ć÷£ŗ”ß”ĻACB=90”ć£¬”ĻADC=90”ć£¬”ĻBEC=90”ć
”ą”ĻACD+”ĻDAC=90”ć£¬”ĻACD+”ĻBCE=90”ć£¬
”ą”ĻDAC=”ĻBCE£¬
ŌŚ”÷ADCÓė”÷CEBÖŠ£¬
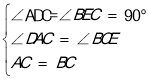 £¬
£¬
”ą”÷ADC”Õ”÷CEB£ØAAS£©£»
¢ŚDE=CE+CD=AD+BE£®ĄķÓÉČēĻĀ£ŗ
ÓÉ¢ŁÖŖ£¬”÷ADC”Õ”÷BEC£¬
”ąAD=CE£¬BE=CD£¬
”ßDE=CE+CD£¬
”ąDE=AD+BE£»
£Ø2£©Ö¤Ć÷£ŗ”ßAD”ĶMNÓŚD£¬BE”ĶMNÓŚE£®
”ą”ĻADC=”ĻBEC=”ĻACB=90”ć£¬
”ą”ĻCAD+”ĻACD=90”ć£¬”ĻACD+”ĻBCE=90”ć£®
”ą”ĻCAD=”ĻBCE£®
ŌŚ”÷ADCŗĶ”÷CEBÖŠ£¬
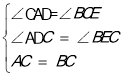 £¬
£¬
”ą”÷ADC”Õ”÷CEB£ØAAS£©£®
”ąCE=AD£¬CD=BE£®
”ąDE=CE©CD=AD©BE£®
£Ø3£©½ā£ŗĶ¬£Ø2£©£¬Ņ×Ö¤”÷ADC”Õ”÷CEB£®
”ąAD=CE£¬BE=CD
”ßCE=CD©ED
”ąAD=BE©ED£¬¼“ED=BE©AD£»
µ±MNŠż×Ŗµ½Ķ¼3µÄĪ»ÖĆŹ±£¬AD”¢DE”¢BEĖłĀś×ćµÄµČĮæ¹ŲĻµŹĒDE=BE©AD£Ø»ņAD=BE©DE£¬BE=AD+DEµČ£©£®


 æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø
æŖŠÄæģĄÖ¼ŁĘŚ×÷ŅµŹī¼Ł×÷ŅµĪ÷°²³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¶ØŅå£ŗŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¹żÅ×ĪļĻß![]() ÓėyÖįµÄ½»µć×÷yÖįµÄ“¹Ļߣ¬Ōņ³ĘÕāĢõ“¹ĻߏĒøĆÅ×ĪļĻߵİéĖęÖ±Ļß.ĄżČē£ŗÅ×ĪļĻß
ÓėyÖįµÄ½»µć×÷yÖįµÄ“¹Ļߣ¬Ōņ³ĘÕāĢõ“¹ĻߏĒøĆÅ×ĪļĻߵİéĖęÖ±Ļß.ĄżČē£ŗÅ×ĪļĻß![]() µÄ°éĖęÖ±ĻßĪŖÖ±Ļß
µÄ°éĖęÖ±ĻßĪŖÖ±Ļß![]() .Å×ĪļĻß
.Å×ĪļĻß![]() µÄ°éĖęÖ±ĻßlÓėøĆÅ×ĪļĻß½»ÓŚµćA”¢D£ØµćAŌŚyÖįÉĻ£©£¬øĆÅ×ĪļĻßÓėxÖįµÄ½»µćĪŖB(-1,0)ŗĶC£ØµćCŌŚµćBµÄÓŅ²ą£©.
µÄ°éĖęÖ±ĻßlÓėøĆÅ×ĪļĻß½»ÓŚµćA”¢D£ØµćAŌŚyÖįÉĻ£©£¬øĆÅ×ĪļĻßÓėxÖįµÄ½»µćĪŖB(-1,0)ŗĶC£ØµćCŌŚµćBµÄÓŅ²ą£©.
£Ø1£©ČōÖ±ĻßlŹĒy=2£¬ĒóøĆÅ×ĪļĻ߶ŌÓ¦µÄŗÆŹż¹ŲĻµŹ½.
£Ø2£©ĒóµćDµÄ×ų±ź£ØÓĆŗ¬mµÄ“śŹżŹ½±ķŹ¾£©.
£Ø3£©ÉčÅ×ĪļĻß![]() µÄ¶„µćĪŖM£¬×÷OAµÄ“¹Ö±Ę½·ÖĻßEF£¬½»OAÓŚµćE£¬½»øĆÅ×ĪļĻߵĶŌ³ĘÖįÓŚµćF.
µÄ¶„µćĪŖM£¬×÷OAµÄ“¹Ö±Ę½·ÖĻßEF£¬½»OAÓŚµćE£¬½»øĆÅ×ĪļĻߵĶŌ³ĘÖįÓŚµćF.
¢Łµ±”÷ADFŹĒµČŃüÖ±½ĒČż½ĒŠĪŹ±£¬ĒóµćMµÄ×ų±ź.
¢Ś½«Ö±ĻßEFŃŲÖ±Ļßl·ÕŪµĆµ½Ö±ĻßGH£¬µ±µćMµ½Ö±ĻßGHµÄ¾ąĄėµČÓŚµćCµ½Ö±ĻßEFµÄ¾ąĄėŹ±£¬Ö±½ÓŠ“³ömµÄÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŅĆĒÖŖµĄ£¬ĪŅĆĒæÉŅŌÓĆ“óŠ“Ó¢ĪÄ×ÖÄø±ķŹ¾Ņ»ĢõĻ߶ĪµÄĮ½øö¶Ėµć£¬±ČČēA£¬B£»ÄĒĆ“ÕāĢõĻ߶ĪæÉŅŌ¼ĒĪŖĻ߶ĪAB£Ø»ņĻ߶ĪBA£©.ČōĻ߶ĪABµÄ³¤µČÓŚ5£¬ĪŅĆĒ±ķŹ¾Ļ߶ĪAB=5.ČōµćP°ŃĻ߶ĪMN·Ö³ÉĻąµČµÄĮ½ĢõĻ߶ĪMPÓėPN£¬Ōņ³ĘµćPĪŖĻ߶ĪMNµÄÖŠµć.øł¾ŻÉĻŹö²ÄĮĻ£¬½ā“šĻĀĮŠĪŹĢā£ŗ
ŅŃÖŖŹżÖįÉĻ£¬µćOĪŖŌµć£¬µćA±ķŹ¾µÄŹżĪŖ8£¬¶ÆµćB£¬CŌŚŹżÖįÉĻŅĘ¶Æ£¬ĒŅ×ܱ£³ÖBC£½2(µćCŌŚµćBÓŅ²ą)£¬ÉčµćB±ķŹ¾µÄŹżĪŖm£®
![]()
![]()
£Ø1£©ČēĶ¼1£¬µ±B£¬CŌŚĻ߶ĪOAÉĻŅĘ¶ÆŹ±£¬
¢Ł ČōBĪŖOAÖŠµć£¬ŌņAC£½ £»
¢Ś ČōB£¬CŅĘ¶Æµ½Ä³Ņ»Ī»ÖĆŹ±£¬Ē”ŗĆĀś×ćAC£½OB£¬Ēó“ĖŹ±mµÄÖµ£»
£Ø2£©µ±Ļ߶ĪBCŌŚŹżÖįÉĻŅĘ¶ÆŹ±£¬Ēė½įŗĻŹżÖį“śŹżŹ½![]() µÄÖµŹĒ·ń“ęŌŚ×īŠ”Öµ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĘä×īŠ”ÖµŗĶ“ĖŹ±mĖłĀś×ćµÄĢõ¼ž£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
µÄÖµŹĒ·ń“ęŌŚ×īŠ”Öµ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĘä×īŠ”ÖµŗĶ“ĖŹ±mĖłĀś×ćµÄĢõ¼ž£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµ![]() ÖŠ£¬ŗÆŹż
ÖŠ£¬ŗÆŹż![]() µÄĶ¼ĻóÓėÖ±Ļß
µÄĶ¼ĻóÓėÖ±Ļß![]() ½»ÓŚµćA(3,m).
½»ÓŚµćA(3,m).
£Ø1£©Ēók”¢mµÄÖµ£»
£Ø2£©ŅŃÖŖµćP(n£¬n)(n>0)£¬¹żµćP×÷Ę½ŠŠÓŚ![]() ÖįµÄÖ±Ļߣ¬½»Ö±Ļßy=x-2ÓŚµćM£¬¹żµćP×÷Ę½ŠŠÓŚyÖįµÄÖ±Ļߣ¬½»ŗÆŹż
ÖįµÄÖ±Ļߣ¬½»Ö±Ļßy=x-2ÓŚµćM£¬¹żµćP×÷Ę½ŠŠÓŚyÖįµÄÖ±Ļߣ¬½»ŗÆŹż![]() µÄĶ¼ĻóÓŚµćN.
µÄĶ¼ĻóÓŚµćN.
¢Łµ±n=1Ź±£¬ÅŠ¶ĻĻ߶ĪPMÓėPNµÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
¢ŚČōPN”ŻPM£¬½įŗĻŗÆŹżµÄĶ¼Ļó£¬Ö±½ÓŠ“³önµÄȔֵ·¶Ī§.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÓėĖıߊĪBEFG¶¼ŹĒÕż·½ŠĪ£¬ÉčAB=a£¬DE=b£Øa£¾b£©£®

£Ø1£©Š“³öAGµÄ³¤¶Č£ØÓĆŗ¬×ÖÄøa”¢bµÄ“śŹżŹ½±ķŹ¾£©£»
£Ø2£©¹Ū²ģĶ¼ŠĪ£¬ŹŌÓĆ²»Ķ¬µÄ·½·Ø±ķŹ¾Ķ¼ŠĪÖŠŅõÓ°²æ·ÖµÄĆ껿£¬ÄćÄÜ»ńµĆĻąÓ¦µÄŅ»øöŅņŹ½·Ö½ā¹«Ź½Āš£æĒė½«Õāøö¹«Ź½Š“³öĄ“£»
£Ø3£©Čē¹ūÕż·½ŠĪABCDµÄ±ß³¤±ČÕż·½ŠĪDEFGµÄ±ß³¤¶ą16cm£¬ĖüĆĒµÄĆ껿Ļą²ī960cm2£®ŹŌĄūÓĆ¢ĘÖŠµÄ¹«Ź½£¬Ēóa”¢bµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»ÉĢµźŌŚÄ³Ņ»Ź±¼äŅŌĆ漞aŌŖ£Øa £¾0£©µÄ¼ŪøńĀō³öĮ½¼žŅĀ·ž£¬ĘäÖŠŅ»¼žÓÆĄū25%£¬ĮķŅ»¼žæ÷Ėš25%.
£Ø1£©µ±a =100Ź±,·ÖĪöĀō³öÕāĮ½¼žŅĀ·ž×ܵďĒÓÆĄū»¹ŹĒæ÷Ėš,»ņŹĒ²»ÓƲ»æ÷£æ
£Ø2£©Š”Ć÷·¢ĻÖ£ŗ²»ĀŪaĪŖŗĪÖµ£¬ÕāŃłĀōĮ½¼žŅĀ·ž×ܵĶ¼ŹĒæ÷Ėš.ĒėÅŠ¶Ļ”°Š”Ć÷·¢ĻÖ”±ŹĒ·ńÕżČ·£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖ»ż¼«ĻģÓ¦ŹŠĪÆÕžø®”°¼Óæģ½ØÉčĢģĄ¶Ė®±ĢµŲĀĢµÄĆĄĄö³¤É³”±µÄŗÅÕŁ£¬ĪŅŹŠÄ³½ÖµĄ¾ö¶Ø“Ó±øŃ”µÄĪåÖÖŹ÷ÖŠŃ”¹ŗŅ»ÖÖ½ųŠŠŌŌÖÖ£®ĪŖĮĖøüŗƵŲĮĖ½āÉēĒéĆńŅā£¬¹¤×÷ČĖŌ±ŌŚ½ÖµĄĻ½Ēų·¶Ī§ÄŚĖ껜³éČ”ĮĖ²æ·Ö¾ÓĆń£¬½ųŠŠ”°ĪŅ×īĻ²»¶µÄŅ»ÖÖŹ÷”±µÄµ÷²é»ī¶Æ£ØĆæČĖĻŽŃ”ĘäÖŠŅ»ÖÖŹ÷£©£¬²¢½«µ÷²é½į¹ūÕūĄķŗ󣬻ęÖĘ³ÉČēĶ¼Į½øö²»ĶźÕūµÄĶ³¼ĘĶ¼£ŗ

Ēėøł¾ŻĖłøųŠÅĻ¢½ā“šŅŌĻĀĪŹĢā£ŗ
£Ø1£©Õā“Ī²ĪÓėµ÷²éµÄ¾ÓĆńČĖŹżĪŖ£ŗ £»
£Ø2£©Ēė½«ĢõŠĪĶ³¼ĘĶ¼²¹³äĶźÕū£»
£Ø3£©Ēė¼ĘĖćÉČŠĪĶ³¼ĘĶ¼ÖŠ”°·ćŹ÷”±ĖłŌŚÉČŠĪµÄŌ²ŠÄ½Ē¶ČŹż£»
£Ø4£©ŅŃÖŖøĆ½ÖµĄĻ½ĒųÄŚĻÖÓŠ¾ÓĆń8ĶņČĖ£¬ĒėÄć¹Ą¼ĘÕā8ĶņČĖÖŠ×īĻ²»¶ÓńĄ¼Ź÷µÄÓŠ¶ąÉŁČĖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ½ā²»µČŹ½×é![]() Ēė½įŗĻĢāŅāĢīæÕ£¬Ķź³É±¾ĢāµÄ½ā“š£®
Ēė½įŗĻĢāŅāĢīæÕ£¬Ķź³É±¾ĢāµÄ½ā“š£®
£Ø¢ń£©½ā²»µČŹ½¢Ł£¬µĆ”” ””£»
£Ø¢ņ£©½ā²»µČŹ½¢Ś£¬µĆ”” ””£»
£Ø¢ó£©°Ń²»µČŹ½¢ŁŗĶ¢ŚµÄ½ā¼ÆŌŚŹżÖįÉĻ±ķŹ¾³öĄ“£®
![]()
£Ø¢ō£©Ō²»µČŹ½×éµÄ½ā¼ÆĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”潫Į½æéĻąĶ¬µÄŗ¬ÓŠ30”ć½ĒµÄČż½Ē³ß°“ČēĶ¼ĖłŹ¾µÄ·½Ź½°Ś·ÅŌŚŅ»Ęš£¬ŌņĖıߊĪABCDĪŖĘ½ŠŠĖıߊĪ£¬ĒėÄ抓³öÅŠ¶ĻµÄŅĄ¾Ż_____£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com