
 已知如图在△ABC中,AB=AC,AD⊥AB,BD=7,AD=3.5,则∠BAC=120°;CD=3.5.
已知如图在△ABC中,AB=AC,AD⊥AB,BD=7,AD=3.5,则∠BAC=120°;CD=3.5. 分析 由AB=AC可知△ABC为等腰三角形,由AD⊥AB,BD=7,AD=3.5,可得∠B=30°,从而可得∠C和∠BAC的度数,从而可以求得CD的长.
解答 解:∵AD⊥AB,
∴∠BAD=90°.
又∵BD=7,AD=3.5,
∴∠B=30°.
∵在△ABC中,AB=AC,
∴∠B=∠C=30°.
∴∠BAC=180°-∠B-∠C=120°.
∴∠DAC=∠BAC-∠BAD=120°-90°=30°.
∴∠DAC=∠C.
∴DA=DC.
∵DA=3.5,
∴CD=3.5.
故答案为:120°,3.5.
点评 本题考查等腰三角形的性质和直角三角形中30°角所对的直角边与斜边的关系,关键是进行灵活变化,找出所求问题需要的条件.


科目:初中数学 来源: 题型:选择题
| A. | 单项式a的系数是0 | |
| B. | 单项式-$\frac{3xy}{5}$的系数和次数分别是-3和2 | |
| C. | 3mn与4nm不是同类项 | |
| D. | 单项式-3πxy2z3的系数和次数分别是-3π和6 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
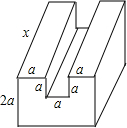 一个工件的形状和部分尺寸如图所示,其体积为a(a+1)(5a+1)+(3a+2)(3a-2)-a+4,求工件的长x是多少(用含a的式子表示).
一个工件的形状和部分尺寸如图所示,其体积为a(a+1)(5a+1)+(3a+2)(3a-2)-a+4,求工件的长x是多少(用含a的式子表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5m2n与-$\frac{1}{3}$nm2 | B. | -4x2y与$\frac{2}{5}$yx2 | C. | -1与$\frac{1}{2}$ | D. | a4y和$\frac{1}{5}$ay4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
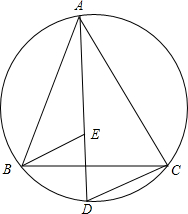 如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.
如图,△ABC的顶点A,B,C都在圆上,$\widehat{AB}$=$\widehat{BC}$=$\widehat{AC}$,D是$\widehat{BC}$上一点,连接AD,在AD上截取AE=DC,试判断△BDE的形状,并说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com