
 如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.
如图,已知正方形ABCD的边长是5,点E在DC上,将△ADE经顺时针旋转后与△ABF重合.分析 (1)根据旋转的定义,直接得出旋转的中心和旋转的角度;
(2)由(1)得到△ADE绕着点A逆时针旋转90°后与△ABF重合,根据旋转的性质得∠FAE=90°,AF=AE,由此可判断△AEF是等腰直角三角形;
(3)利用旋转中心为正方形对角线的交点,逆时针旋转90°(或逆时针旋转270°),即可得出平移距离等于正方形边长;
(4)根据平移的性质得AF∥DH,由(2)得AF⊥AE,所以AE⊥DH,进而得出AE=DH.
解答 解:(1)旋转的中心是点A,旋转的角度是90°;
(2)△AEF是等腰直角三角形.
理由如下:
∵△ADE绕点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴△AEF是等腰直角三角形.
(3)∵正方形ABCD的边长是5,
∴△ABF向右平移后与△DCH位置,平移的距离是5;
(4)AE=DH,AE⊥DH,
理由:∵△ABF向右平移后与△DCH重合,
∴DH∥AF,DH=AF,
又∵△ADE绕着点A顺时针旋转90°后与△ABF重合,
∴∠FAE=∠BAD=90°,AF=AE,
∴AE⊥AF,
∴AE=DH,AE⊥DH.
点评 本题考查了四边形综合以及正方形的性质、等腰直角三角形的判定和平移的性质、旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;对应点与旋转中心的连线段的夹角等于旋转角.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源: 题型:选择题
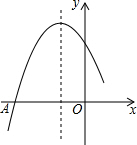 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )| A. | b2<4ac | |
| B. | 2a+b=0 | |
| C. | a+b+c>0 | |
| D. | 若点B($\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测验 类别 | 平时测验 | 期中 测验 | 期末 测验 | |||
| 第1次 | 第2此 | 第3次 | 第4次 | |||
| 成绩 | 80 | 86 | 84 | 90 | 90 | 95 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com