
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调查.
问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.

请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;补全条形统计图;
(2)求出C类人数占总调查人数的百分比及扇形统计图中![]() 类所对应扇形圆心角的度数.
类所对应扇形圆心角的度数.
【答案】(1)50;(2)108°.
【解析】试题分析:(1)用B类的人数除以其所占的百分比可得到样本容量;用样本容量减去A、B、D类的人数可求得C类的人数,进而补全条形统计图;
(2)用C类人数除以总人数得到C类人数占总调查人数的百分比;用A类人数除以总人数得到A类所占的百分比,然后乘以360°,即可得出A类所对应扇形圆心角的度数.
试题解析:解:(1)该班参与问卷调查的人数有:20÷40%=50(人),C类的人数为:50﹣15﹣20﹣5=10(人),条形统计图补充如下:
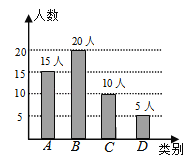
(2)C类人数占总调查人数的百分比是:10÷50=20%,扇形统计图中A类所对应扇形圆心角的度数是:15÷50×360°=108°.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )
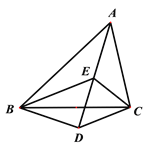
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB=7°,一条光线从点A出发后射向OB边.若光线与OB边垂直,则光线沿原路返回到点A,此时∠A=90°-7°=83°.当∠A<83°时,光线射到OB边上的点A1后,经OB反射到线段AO上的点A2,易知∠1=∠2.若A1A2⊥AO,光线又会沿A2→A1→A原路返回到点A,此时∠A=76°.…若光线从A点出发后,经若干次反射能沿原路返回到点A,则锐角∠A的最小值为______.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把四块长为a,宽为b的长方形木板围成如图所示的正方形,请解答下列问题:
(1)按要求用含a,b的式子表示空心部分的正方形的面积S(结果不要化简,保留原式):
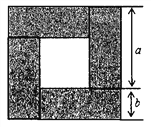
①用大正方形面积减去四块木板的面积表示:S= ;
②直接用空心部分的正方形边长的平方表示:S= ;
(2)由①、②可得等式 ;
(3)用整式的乘法验证(2)中的等式成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)已知△ABC是等边三角形,点D是直线BC上一点,以AD为一边在AD的右侧作等边△ADE.
(1)如图①,点D在线段BC上移动时,直接写出∠BAD和∠CAE的大小关系;
(2)如图②,点D在线段BC的延长线上移动时,猜想∠DCE的大小是否发生变化.若不变请求出其大小;若变化,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我省启动了“关爱留守儿童工程”.某村小为了了解各年级留守儿童的数量,对一到六年级留守儿童数量进行了统计,得到每个年级的留守儿童人数分别为10,15,10,17,18,20.对于这组数据,下列说法错误的是( )
A.平均数是15 B.众数是10 C.中位数是17 D.方差是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把一个菱形绕着它的对角线的交点旋转![]() ,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为
,旋转前后的两个菱形构成一个“星形”(阴影部分).若菱形的一个内角为![]() ,边长为
,边长为![]() ,则该“星形”的面积是__________.
,则该“星形”的面积是__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com