
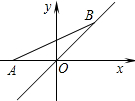
 如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )
如图,点A的坐标为(-2,0),点B在直线y=x上运动,当线段AB最短时点B的坐标为( )| A. | (0,0) | B. | (-1,-1) | C. | ($\sqrt{2}$,-$\sqrt{2}$) | D. | (-$\sqrt{2}$,-$\sqrt{2}$) |
分析 过点A作AD⊥OB于点D,过点D作DE⊥x轴于点E,先根据垂线段最短得出当点B与点D重合时线段AB最短,再根据直线OB的解析式为y=x得出△AOD是等腰直角三角形,故DE=$\frac{1}{2}$OA=1,由此可得出结论.
解答 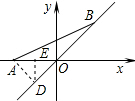 解:过点A作AD⊥OB于点D,过点D作DE⊥x轴于点E,
解:过点A作AD⊥OB于点D,过点D作DE⊥x轴于点E,
∵垂线段最短,
∴当点B与点D重合时线段AB最短.
∵直线OB的解析式为y=x,
∴△AOD是等腰直角三角形,
∴DE=$\frac{1}{2}$OA=1,
∴D(-1,-1).
故选B.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 动手操作:在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P,Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )
动手操作:在矩形纸片ABCD中,AB=6,AD=10.如图所示,折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P、Q也随之移动.若限定点P,Q分别在AB、AD边上移动,则点A′在BC边上可移动的最大距离为( )| A. | 4cm | B. | 6cm | C. | 8cm | D. | 10cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
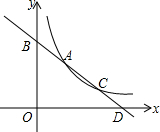 如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).
如图,一次函数y=-$\frac{\sqrt{3}}{2}$x+3$\sqrt{3}$与反比例函数y=$\frac{a}{x}$的图象交于点A(2,2$\sqrt{3}$),点C(4,b).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
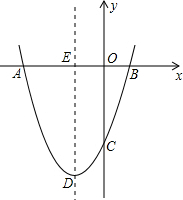 如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).
如图,抛物线y=ax2+bx+c经过点A(-6,0),B(2,0),C(0,-6).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com