
【题目】解分式方程、分式的化简求值
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ,其中
,其中![]() ;
;
(4) ,其中x是不等式组
,其中x是不等式组 的解集中符合题意的整数.
的解集中符合题意的整数.
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,把△ABC绕AC边的中点M旋转后得△DEF,若直角顶点F恰好落在AB边上,且DE边交AB边于点G,若AC=4,BC=3,则AG的长为( )

A.![]() B.
B.![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣4x与x轴交于O,A两点,P为抛物线上一点,过点P的直线y=x+m与对称轴交于点Q.
(1)这条抛物线的对称轴是 ,直线PQ与x轴所夹锐角的度数是 ;
(2)若两个三角形面积满足S△POQ=![]() S△PAQ,求m的值;
S△PAQ,求m的值;
(3)当点P在x轴下方的抛物线上时,过点C(2,2)的直线AC与直线PQ交于点D,求:①PD+DQ的最大值;②PDDQ的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市2013年启动省级园林城市创建工作,计划2015年下半年顺利通过验收评审.该市为加快道路绿化及防护绿地等各项建设.在城市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD的边长为3,E、F分别是AB、BC边上的点,且∠EDF=45°.将△DAE绕点D逆时针旋转90°,得到△DCM.
(1)求证:EF=FM
(2)当AE=1时,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两市相距150千米,分别从A、B处测得国家级风景区中心C处的方位角如图所示,风景区区域是以C为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部门设计修建连接AB两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从A、B两地同时出发匀速相向而行,大楼C位于AB之间,甲与乙相遇在AC中点处,然后两车立即掉头,以原速原路返回,直到各自回到出发点.设甲、乙两车距大楼C的距离之和为y(千米),甲车离开A地的时间为t(小时),y与t的函数图象所示,则第21小时时,甲乙两车之间的距离为________千米.

查看答案和解析>>
科目:初中数学 来源: 题型:
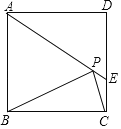
【题目】如图,在正方形ABCD中,AD=2![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com