
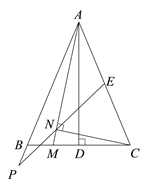
【题目】在锐角△ABC中,AB=AC,AD为BC边上的高,E为AC中点.
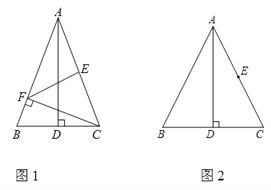
(1)如图1,过点C作CF⊥AB于F点,连接EF.若∠BAD=20°,求∠AFE的度数;
(2)若M为线段BD上的动点(点M与点D不重合),过点C作CN⊥AM于N点,射线EN,AB交于P点.
①依题意将图2补全;
②小宇通过观察、实验,提出猜想:在点M运动的过程中,始终有∠APE=2∠MAD.
小宇把这个猜想与同学们进行讨论,形成了证明该猜想的几种想法:
想法1:连接DE,要证∠APE=2∠MAD,只需证∠PED=2∠MAD.
想法2:设∠MAD=α,∠DAC=β,只需用α,β表示出∠PEC,通过角度计算得∠APE=2α.
想法3:在NE上取点Q,使∠NAQ=2∠MAD,要证∠APE=2∠MAD,只需证△NAQ∽△APQ.……
请你参考上面的想法,帮助小宇证明∠APE =2∠MAD.(一种方法即可)
【答案】(1)证明见解析;(2)① 补图见解析;②证明见解析.
【解析】(1)证明:∵AB=AC,AD为BC边上的高,∠BAD=20°,
∴∠BAC=2∠BAD=40°.
∵CF⊥AB, ∴∠AFC=90°.
∵E为AC中点,
∴EF=EA= ![]() .
.
∴∠AFE=∠BAC=40°.
(2)①
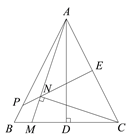
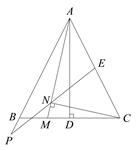
画出一种即可.
②证明:
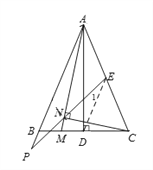
想法1:连接DE.
∵AB=AC,AD为BC边上的高,
∴D为BC中点.
∵E为AC中点,
∴ED∥AB,
∴∠1=∠APE.
∵∠ADC=90°,E为AC中点,
∴![]() .
.
同理可证![]() .
.
∴AE=NE=CE=DE.
∴A,N,D,C在以点E为圆心,AC为直径的圆上.
∴∠1=2∠MAD.
∴∠APE=2∠MAD.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD. 
求证:
(1)△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在创建全国森林城市的活动中,我区一“青年突击队”决定义务整修一条1000米长的绿化带,开工后,附近居民主动参加到义务劳动中,使整修的速度比原计划提高了一倍,结果提前4小时完成任务,问“青年突击队”原计划每小时整修多少米长的绿化带?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出1000张票,筹出票款6920元,且每张成人票8元,学生票5元.
(1)问成人票与学生票各售出多少张?
(2)若票价不变,仍售出1000张票,所得的票款可能是7290元吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为弦,D为![]() 的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.
的中点,AC,BD相交于E点,过点A作⊙O的切线交BD的延长线于P点.

(1)求证:∠PAC=2∠CBE;
(2)若PD=m,∠CBE=α,请写出求线段CE长的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:

请结合图表完成下列各题:
(1)①表中a的值为 ; ②频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是
(3)第5组10名同学中,有4名男同学,现将这10名同学平均分成两组进行对抗练习,且4名男同学每组分两人,求小明与小强两名男同学能分在同一组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
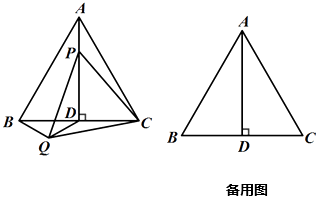
【题目】如图,正△ABC 中,高线 ![]() ,点
,点 ![]() 从点
从点 ![]() 出发,沿着
出发,沿着 ![]() 运动到点
运动到点 ![]() 停止,以
停止,以 ![]() 为边向左下方作正
为边向左下方作正 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
(1)求证: ![]() ≌
≌ ![]() ;
;
(2)在点P的运动过程中,当 ![]() 是等腰三角形时,求
是等腰三角形时,求 ![]() 的度数;
的度数;
(3)直接写出在点 P的运动过程中, ![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com