
(本小题满分10分)已知直线y=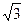 x+4
x+4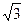 与x轴,y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
与x轴,y轴分别交于A、B两点,∠ABC=60°,BC与x轴交于点C.
(1)试确定直线BC的解析式.
(2)若动点P从A点出发沿AC向点C运动(不与A、C重合),同时动点Q从C点出发
沿CBA向点A运动(不与C、A重合) ,动点P的运动速度是每秒1个单位长度,动点Q
的运动速度是每秒2个单位长度.设△APQ的面积为S,P点的运动时间为t秒,求S与t的
函数关系式,并写出自变量的取值范围.
(3)在(2)的条件下,当△ APQ的面积最大时,y轴上有一点M,平面内是否存在一点
APQ的面积最大时,y轴上有一点M,平面内是否存在一点
N,使以A、Q、M、N为顶点的四边形为菱形?若存在,请直接写出N点的坐标;若不存
在,请说明理由.
(本小题满分10分)解:( 1 )由已知得A点坐标(-4﹐0),B点坐标(0﹐4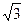 ﹚
﹚
∵OA=4 OB=4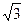
∴∠BAO=60º
∵∠ABC=60º
∴△ABC是等边三角形
∵OC=OA=4
∴C点坐标﹙4,0﹚
设直线BC解析式为y=kx﹢b ∴
∴
∴直线BC的解析式为y=- ------------------------------------------ (2分)
------------------------------------------ (2分)
﹙2﹚当P点在AO之间运动时,作QH⊥x轴。
∵
∴ ∴QH=
∴QH=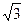 t
t
∴S△APQ=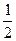 AP·QH=
AP·QH=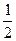 t·
t·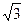 t=
t= t²(0<t≤4)---------------------------------------(2分)
t²(0<t≤4)---------------------------------------(2分)
同理可得S△APQ=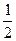 t·﹙8
t·﹙8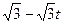 ﹚=-
﹚=- ﹙4≤t<8﹚--------------(2分)
﹙4≤t<8﹚--------------(2分)
(3)存在,(4,0),(-4,8)(-4,-8)(-4, ) ----------------------(4分)
) ----------------------(4分)
解析


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
 .
.查看答案和解析>>
科目:初中数学 来源:2011年河北省中考模拟试卷数学卷 题型:解答题
(本小题满分10分)
如图,在平面直角坐标系中,直线L:y=-2x-8分别与x轴、y轴相交于A、B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P。
(1)连结PA,若PA=PB,试判断⊙P与X轴的位置关系,并说明理由;
(2)当K为何值时,以⊙P与直线L的两个交点和圆心P为顶点的三角形是正三角形?
查看答案和解析>>
科目:初中数学 来源:2011年四川省盐源县民族中学中考模拟试题数学卷 题型:解答题
(本小题满分10分)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
【小题1】(1)求梯形ABCD的面积;
【小题2】(2)当P点离开D点几秒后,PQ//AB;
【小题3】(3)当P、Q、C三点构成直角三角形时,求点P从点D运动的时间?
查看答案和解析>>
科目:初中数学 来源:2011-2012年河北省衡水市五校九年级第三次联考数学卷 题型:解答题
(本小题满分10分)如图,在平面直角坐标系中,点A、B、C、P的坐标分别为(0,1)、(-1,0)、(1,0)、(-1,-1)。
【小题1】(1)求经过A、B、C三点的抛物线的表达式;
【小题2】(2)以P为位似中心,将△ABC放大,使得放大后的△A1B1C1
与△OAB对应线段的比为3:1,请在右图网格中画出放大
后的△A1B1C1;(所画△A1B1C1与△ABC在点P同侧);
【小题3】(3)经过A1、B1、C1三点的抛物线能否由(1)中的抛物线平
移得到?请说明理由。
查看答案和解析>>
科目:初中数学 来源:2012届河南省商丘市九年级上学期期末考试数学卷 题型:解答题
(本小题满分10分)
在图1至图3中,直线MN与线段AB相交
于点O,∠1 = ∠2 = 45°.
【小题1】(1)如图1,若AO = OB,请写出AO与BD
的数量关系和位置关系;
【小题2】(2)将图1中的MN绕点O顺时针旋转得到
图2,其中AO = OB.
求证:AC = BD,AC ⊥ BD;
【小题3】(3)将图2中的OB拉长为AO的k倍得到
图3,求 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com