
分析 先通分,再进行同分母的加法运算,然后把分子分母因式分解后约分得到原式=$\frac{2n+m}{2n-m}$,再把n=5m代入计算即可.
解答 解:原式=$\frac{2n(2n-m)}{(2n+m)(2n-m)}$+$\frac{m(2n+m)}{(2n+m)(2n-m)}$+$\frac{4mn}{(2n+m)(2n-m)}$
=$\frac{4{n}^{2}-2mn+2mn+{m}^{2}+4mn}{(2n+m)(2n-m)}$
=$\frac{(2n+m)^{2}}{(2n+m)(2n-m)}$
=$\frac{2n+m}{2n-m}$,
当m=$\frac{1}{5}$n,即n=5m时,原式=$\frac{10m+m}{10m-m}$=$\frac{11}{9}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.


科目:初中数学 来源: 题型:解答题
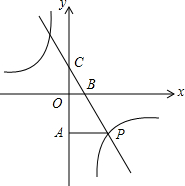 如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.
如图,一次函数y=kx+3的图象分别交x轴、y轴于点B、点C,与反比例函数y=$\frac{n}{x}$的图象在第四象限的相交于点P,并且PA⊥y轴于点A,已知A (0,-6),且S△CAP=18.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
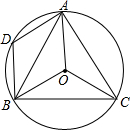 如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.
如图,在⊙0中,$\widehat{AB}$=$\widehat{AC}$,∠ACB=60°.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
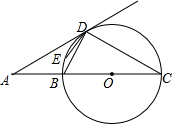 如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.
如图,BC是⊙O的直径,延长CB到点A使AB=$\frac{1}{2}$CB,过点A作射线AD,使AD与⊙O相切于点D,连接BD,CD.若点E是劣弧$\widehat{BD}$上一点,则∠BED的度数为150°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
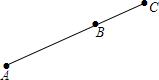 如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.
如图,A、B、C是一条公路边的三个连锁超市,且A、B、C在一条直线上,计划在A、C之间的公路边建一个配货中心P,负责向3个超市送货.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com