
 将两块直角三角板按如图所示方式摆放,则△ABO与△CDO的面积比为
将两块直角三角板按如图所示方式摆放,则△ABO与△CDO的面积比为| 3 |
| 3 |
| S△ABO |
| S△CDO |
| AB |
| CD |
| a2 |
| 3a2 |
| 1 |
| 3 |


 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市南长区九年级上学期期末考试数学试卷(解析版) 题型:解答题
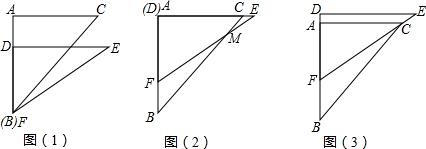
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,∠FDE=90°,DF=4,DE=4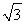 ,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
,将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.

(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= ?? 度;

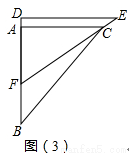
(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,当D在BA的延长线上时,设BF=x,两块三角板重迭部分的面积为y.求y与x的函数关系式,并求出对应的x取值范围.
查看答案和解析>>
科目:初中数学 来源:2013年广东省中考数学试卷(解析版) 题型:解答题
 .将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.
.将这副直角三角板按如图1所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上.现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动.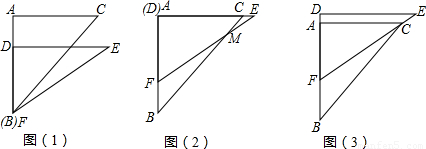
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(广东卷)数学(解析版) 题型:解答题
有一副直角三角板,在三角板ABC中,∠BAC=90°,AB=AC=6,在三角板DEF中,
∠FDE=90°,DF=4,DE=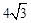 。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。
。将这副直角三角板按如图(1)所示位置摆放,点B与点F重合,直角边BA与FD在同一条直线上,现固定三角板ABC,将三角板DEF沿射线BA方向平行移动,当点F运动到点A时停止运动。

(1)如图(2),当三角板DEF运动到点D与点A重合时,设EF与BC交于点M,则∠EMC= 度;

(2)如图(3),在三角板DEF运动过程中,当EF经过点C时,求FC的长;
(3)在三角板DEF运动过程中,设BF=x,两块三角板重叠部分面积为y,求y与x的函数解析式,并求出对应的x取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com