
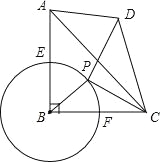
【题目】如图,在等腰直角三角形ABC中,∠ABC=90°,AB=BC=4,⊙B与AB、BC交于E、F,点P是弧EF上的一个动点,连接PC,线段PC绕P点逆时针旋转90°到PD,连接CD,AD.
(1)求证:△BPC∽△ADC;
(2)当四边形ABCD满足AD∥CB且是面积为12时,求⊙B的半径;
(3)若⊙B的半径的为2,当点P沿弧EF从点E运动至点PC与⊙B相切时,求点D的运动路径的长.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)由等腰直角三角形的性质可知:BC:AC=PC:DC,∠PCD=∠ACB,从而可证明∠BCP=∠ACD,最后依据两边对应成比例且夹角相等的两三角形相似进行证明即可;
(2)如图1所示:先求得△ABC的面积,然后可得到△ADC的面积,依据三角形的面积公式可得到AD的长,然后依据相似三角形对应边长比例可求得PB的长;
(3)如图2所示:由相似三角形的性质可知:AD=2![]() ,于是可得到点D在以A为圆心,以2
,于是可得到点D在以A为圆心,以2![]() 为半径的圆上,然后根据点P在圆B的运动路线和确定点D经过的路径(弧)所对的圆心角,最后依据弧长公式求解即可.
为半径的圆上,然后根据点P在圆B的运动路线和确定点D经过的路径(弧)所对的圆心角,最后依据弧长公式求解即可.
试题解析:(1)∵∠ABC=90°,AB=BC,
∴∠ACB=45°,BC:AC=1:![]() .
.
∵PD=PC,∠DPC=90°,
∴∠PCD=45°,PC:DC=1:![]() .
.
∴BC:AC=PC:DC,∠PCD=∠ACB.
∴∠PCD﹣∠PCA=∠ACB﹣∠PCA,即∠BCP=∠ACD.
∴△BPC∽△ADC.
(2)如图1所示:

∵AB=BC=4,∠ABC=90°,
∴S△ABC=![]() ABBC=
ABBC=![]() ×4×4=8,
×4×4=8,
∵四边形ABCD的面积为12,
∴S△ADC=4.
∵AD∥BC,
∴S△ADC=![]() ADAB=4,即
ADAB=4,即![]() ×4×AD=4.
×4×AD=4.
∴AD=2.
∵△BPC∽△ADC,
∴![]() ,
,
即![]() .
.
解得BP=![]() .
.
∴⊙B的半径为![]() .
.
(3)如图2所示:

∵BP=2,由(2)可知AD:BP=![]() :1,
:1,
∴AD=2![]() .
.
∴D在以A为圆心,以2![]() 为半径的圆上.
为半径的圆上.
∵△BPC∽△ADC,
∴∠PBC=∠DAC.
∵当点P与点E重合时,∠PBC=90°.
∴∠DAC=90°.
当点P′C与圆B相切时,∠BP′C=90°,BP′=2,BC=4,
∴∠P′BC=60°.
span>∴∠D′AC=60°.
∴∠D′AD=90°﹣60°=30°.
∴点D运动的路线长=![]() =
=![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】你能求(x﹣1)(x99+x98+x97+…+x+1)的值吗?
遇到这样的问题,我们可以先思考一下,从简单的情形入手.先计算下列各式的值:
(1)(x﹣1)(x+1)=;
(2)(x﹣1)(x2+x+1)=;
(3)(x﹣1)(x3+x2+x+1)=;
由此我们可以得到(x﹣1)(x99+x98+…+x+1)=;
请你利用上面的结论,完成下面两题的计算:
(1)299+298+…+2+1;
(2)(﹣3)50+(﹣3)49+…+(﹣3)+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系xOy中,点B(﹣2,2),过反比例函数y=![]() (x<0,常数k<0)图象上一点A(﹣
(x<0,常数k<0)图象上一点A(﹣![]() ,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
,m)作y轴的平行线交直线l:y=x+2于点C,且AC=AB.
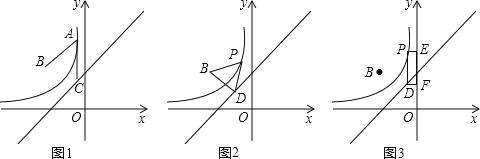
(1)分别求出m、k的值,并写出这个反比例函数解析式;
(2)发现:过函数y=![]() (x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
(x<0)图象上任意一点P,作y轴的平行线交直线l于点D,请直接写出你发现的PB,PD的数量关系 ;
应用:①如图2,连接BD,当△PBD是等边三角形时,求此时点P的坐标;
②如图3,分别过点P、D作y的垂线交y轴于点E、F,问是否存在点P,使得矩形PEFD的周长取得最小值?若存在,请求出此时点P的坐标及矩形PEFD的周长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
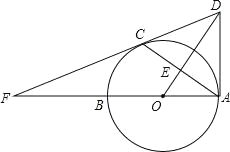
【题目】如图,已知AB是⊙O的直径,C是⊙O上的点,且OE⊥AC于点E,过点C作⊙O的切线,交OE的延长线于点D,交AB的延长线于点F,连接AD.(1)求证:AD是⊙O的切线;
(2)若cos∠BAC=![]() ,AC=8,求线段AD的长.
,AC=8,求线段AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】可乐和奶茶含有大量的咖啡因,世界卫生组织建议青少年每天摄入的咖啡因不能超过0.000085kg,将数据0.000085用科学记数法表示为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学5次数学小测验的成绩分别为(单位:分):90,85,90,95,100,则该同学这5次成绩的众数是( )
A.90 分B.85 分C.95 分D.100 分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小组7位学生的中考体育测试成绩(满分30分)依次为27,30,29,27,30,28,30.则这组数据的众数与中位数分别是( )
A.30,27
B.30,29
C.29,30
D.30,28
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com