
【题目】如图1,在菱形ABCD中,点E,F分别为AB,AD的中点,连结CE,CF.

(1)求证:CE=CF;
(2)如图2,若H为AB上一点,连结CH,使∠CHB=2∠ECB,求证:CH=AH+AB.
【答案】(1)见解析;(2)见解析
【解析】
(1)由菱形ABCD中,点E、F分别为AB、AD的中点,易证得△BCE≌△DCF(SAS),则可得CE=CF;
(2)由平行线的性质,可得AG=AB,∠G=∠FCD,由全等三角形的对应角相等,可得∠BCE=∠DCF,然后由∠CHB=2∠ECB,易证得∠G=∠HCG,则可得CH=GH,则可证出结果.
(1)证明:∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,
∵点E、F分别为AB、AD的中点,
∴BE=![]() AB,DF=
AB,DF=![]() AD,
AD,
∴BE=DF,
在△BCE和△DCF中,
 ,
,
∴△BCE≌△DCF(SAS),
∴CE=CF;
(2)证明:延长BA与CF,交于点G,
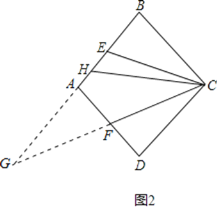
∵四边形ABCD是菱形,
∴∠B=∠D,AB=BC=CD=AD,AF∥BC,AB∥CD,
∴∠G=∠FCD,
∵点F分别为AD的中点,且AG∥CD,
∴AG=AB,
∵△BCE≌△DCF,
∴∠ECB=∠DCF,
∵∠CHB=2∠ECB,
∴∠CHB=2∠G,
∵∠CHB=∠G+∠HCG,
∴∠G=∠HCG,
∴GH=CH,
∴CH=AH+AG=AH+AB.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
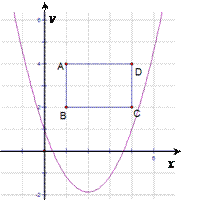
【题目】如图,二次函数![]() 的图象经过点(0,1)坐标平面内有矩形ABCD,A(1,4),B(1,2)C(4,2),D(4,4)
的图象经过点(0,1)坐标平面内有矩形ABCD,A(1,4),B(1,2)C(4,2),D(4,4)
(1)用a表示k;
(2)试说明抛物线图象一定经过(4,1);
(3)求抛物线顶点在x轴上方时,a的取值范围;
(4)写出抛物线与矩形ABCD各边交点个数与a的对应取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分)如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于点D,过点D作DE⊥MN于点E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
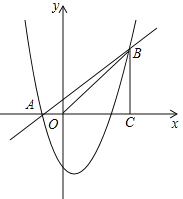
【题目】如图,已知抛物线![]() 经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
经过A(-1,0)、B(4,5)两点,过点B作BC⊥x轴,垂足为C.
(1)求抛物线的解析式;
(2)求tan∠ABO的值;
(3)点M是抛物线上的一个点,直线MN平行于y轴交直线AB于N,如果以M、N、B、C为顶点的四边形是平行四边形,求出点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工艺厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况(超产记为正、减产记为负):

(1)写出该厂星期一生产工艺品的数量;
(2)本周产量最多的一天比最少的一天多生产多少个工艺品?
(3)请求出该工艺厂在本周实际生产工艺品的数量;
(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个另奖50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简:
(1)3b+5a-(2a-4b )
(2)化简求值:7a2b+2(2a2b-3ab2)-(4a2b-ab2),其中a,b满足|a+2|+(b![]() )2 =0
)2 =0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按如图所示的程序计算,若开始输入的x的值为10,则第一次输出的结果是5,第二次输出的结果是8,……,以此类推,第2019次输出的结果是______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com