
 已知二次函数图象的顶点坐标为(0,1),且过点(-1,$\frac{5}{4}$),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1,y1),B(x2,y2).
已知二次函数图象的顶点坐标为(0,1),且过点(-1,$\frac{5}{4}$),直线y=kx+2与y轴相交于点P,与二次函数图象交于不同的两点A(x1,y1),B(x2,y2).分析 (1)设二次函数解析式为y=ax2+1,由于点(-1,$\frac{5}{4}$)在二次函数图象上,把该点的坐标代入y=ax2+1,即可求出a,从而求出二次函数的解析式.
(2)先分别求出x=-1,x=0,x=3时y的值,然后结合图象就可得到y的取值范围.
(3)过点A作y轴的对称点A′,连接BA′并延长,交y轴于点G,连接AG,如图2,则点A′必在抛物线上,且∠AGP=∠BGP,由此可得△ABG的内切圆的圆心落在y轴上.由于点A(x1,y1)、B(x2,y2)在直线y=kx+2上,从而可以得到点A的坐标为(x1,kx1+2)、A′的坐标为(-x1,kx1+2)、B的坐标为(x2,kx2+2).设直线BG的解析式为y=mx+n,则点G的坐标为(0,n).由于点A′(-x1,kx1+2)、B(x2,kx2+2)在直线BG上,可用含有k、x1、x2的代数式表示n.由于A、B是直线y=kx+2与抛物线y=$\frac{1}{4}$x2+1的交点,由根与系数的关系可得:x1+x2=4k,x1•x2=-4.从而求出n=0,即可证出:在此二次函数图象下方的y轴上,存在定点G(0,0),使△ABG的内切圆的圆心落在y轴上.由S△ABG=S△APG+S△BPG,可以得到S△ABG即可用k表示,从而求得最小值.
解答 (1)解:由于二次函数图象的顶点坐标为(0,1),
因此二次函数的解析式可设为y=ax2+1.
∵抛物线y=ax2+1过点(-1,$\frac{5}{4}$).
解得:a=$\frac{1}{4}$.
∴二次函数的解析式为:y=$\frac{1}{4}$x2+1;
(2)解:当x=-1时,y=$\frac{5}{4}$,当x=0时,y=1,
当x=3时,y=$\frac{13}{4}$结合图1可得:当-1<x<3时,y的取值范围是1≤y<$\frac{13}{4}$;
(3)①证明:∵△ABG的内切圆的圆心落在y轴上,
∴GP平分∠AGB.
∴直线GP是∠AGB的对称轴.
过点A作GP的对称点A′,如图2,
则点A′一定在BG上.
∵点A的坐标为(x1,y1),
∴点A′的坐标为(-x1,y1).
∵点A(x1,y1)、B(x2,y2)在直线y=kx+2上,
∴y1=kx1+2,y2=kx2+2.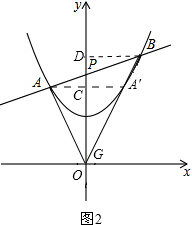
∴点A′的坐标为(-x1,kx1+2)、点B的坐标为(x2,kx2+2).
设直线BG的解析式为y=mx+n,则点G的坐标为(0,n).
∵点A′(-x1,kx1+2)、B(x2,kx2+2)在直线BG上,
∴$\left\{\begin{array}{l}{-{x}_{1}m+n=k{x}_{1}+2}\\{{x}_{2}m+n=k{x}_{2}+2}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{m=\frac{k({x}_{2}-{x}_{1})}{{x}_{2}+{x}_{1}}}\\{n=\frac{2k{x}_{1}{x}_{2}}{{x}_{2}+{x}_{1}}+2}\end{array}\right.$.
∵A(x1,y1),B(x2,y2)是直线y=kx+2与抛物线y=$\frac{1}{4}$x2+1的交点,
∴x1、x2是方程kx+2=$\frac{1}{4}$x2+1即x2-4kx-4=0的两个实数根.
∴由根与系数的关系可得;x1+x2=4k,x1•x2=-4.
∴n=$\frac{2k×(-4)}{4k}$=-2+2=0.
∴点G的坐标为(0,0).
∴在此二次函数图象下方的y轴上,存在定点G(0,0),使△ABG的内切圆的圆心落在y轴上.
②解:过点A作AC⊥OP,垂足为C,过点B作BD⊥OP,垂足为D,如图2,
∵直线y=kx+2与y轴相交于点P,
∴点P的坐标为(0,2).
∴PG=2.
∴S△ABG=S△APG+S△BPG
=$\frac{1}{2}$PG•AC+$\frac{1}{2}$PG•BD
=$\frac{1}{2}$PG•(AC+BD)
=$\frac{1}{2}$×2×(-x1+x2)
=x2-x1
=$\sqrt{({x}_{2}-{x}_{1})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{(4k)^{2}-4×(-4)}$
=$\sqrt{16({k}^{2}+1)}$
=4$\sqrt{{k}^{2}+1}$.
∴当k=0时,S△ABG最小,最小值为4.
∴△GAB面积的最小值为4.
点评 本题考查了用待定系数法求二次函数及一次函数的解析式、二次函数的图象、三角形的内切圆、根与系数的关系、完全平方公式等知识,综合性比较强,有一定的难度.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
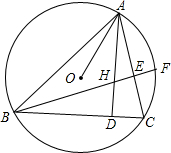 如图,△ABC的三个顶点都在⊙O上,AD、BE是△ABC的高,交于点H,BE的延长线交⊙O于F,下列结论:
如图,△ABC的三个顶点都在⊙O上,AD、BE是△ABC的高,交于点H,BE的延长线交⊙O于F,下列结论:| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com