解:(1)设y=kx+b,把(56,128)和(65,110)分别代入得:

,
解得:
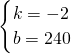
,
∴y与x的关系式为y=-2x+240;
(2)由题意知:w=(x-50)•y=(x-50)•(-2x+240)=-2x
2+340x-12000,
∴w与x的关系式为:y=-2x
2+340x-12000,
∵w=-2x
2+340x-12000=-2(x-85)
2+2450,
∴当x=85时,在50<x≤90内,w的值最大为2450元;
(3)若公司想获得不低于2250元周利润,则w=-2x
2+340x-12000≥2250
即w′=-2x
2+340x-14250,
∵物价部门规定茶叶销售单价不得高于90元/千克,
∴销售单价范围为:75≤x≤90.
分析:(1)有函数的图象可知y与x是一次函数的关系,所以可设y=kx+b,把(56,128)和(65,110)分别代入求出k和b的值即可;
(2)利用每千克销售利润×销售量=总销售利润列出函数关系式,整理即可解答,再利用配方法即可求出如何定价每周获得利润最大,和周最大利润是多少;
(3)有(2)可得w和x的关系式,根据题目的条件画出图象,结合图象确定销售单价范围即可.
点评:本题考查的是二次函数和二次函数的实际应用.求二次函数的最大(小)值有三种方法,第一种可由图象直接得出,第二种是配方法,第三种是公式法,常用的是后两种方法.

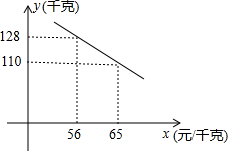 千克)与销售单价x(元/千克)关系如图所示,解答下列问题:
千克)与销售单价x(元/千克)关系如图所示,解答下列问题: ,
,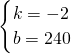 ,
,
