
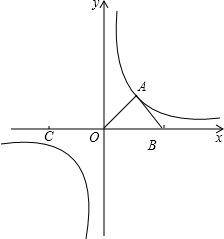
如图,点P在第一象限,△ABP是边长为2的等边三角形, 
当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴
上运动,运动过程中,点P到原点的最大距离是________;
若将△ABP的PA边长改为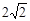 ,另两边长度不变,则点P
,另两边长度不变,则点P
到原点的最大距离变为________.
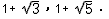
解析考点:直角三角形斜边上的中线;坐标与图形性质;三角形三边关系;等边三角形的性质;勾股定理的逆定理.
分析:根据当O到AB的距离最大时,OP的值最大,得到O到AB的最大值是 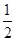 AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为2
AB=1,此时在斜边的中点M上,由勾股定理求出PM,即可求出答案;将△ABP的PA边长改为2
,另两边长度不变,根据22+22="(2" 2 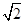 )2,得到∠PBA=90°,由勾股定理求出PM即可
)2,得到∠PBA=90°,由勾股定理求出PM即可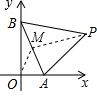
解:取AB的中点M,连OM,PM,
在Rt△ABO中,OM=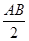 =1,在等边三角形ABP中,PM=
=1,在等边三角形ABP中,PM=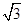 ,
,
无论△ABP如何运动,OM和PM的大小不变,当OM,PM在一直线上时,P距O最远,
∵O到AB的最大值是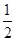 AB=1,
AB=1,
此时在斜边的中点M上,
由勾股定理得:PM=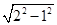 =
=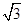 ,
,
∴OP=1+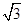 ,
,
将△AOP的PA边长改为2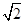 ,另两边长度不变,
,另两边长度不变,
∵22+22=(2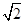 )2,
)2,
∴∠PBA=90°,由勾股定理得:PM=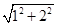 =
= ,
,
∴此时OP=OM+PM=1+ .
.
故答案为:1+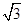 ,1+
,1+ .
.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
 26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.
26、点P为抛物线y=x2-2mx+m2(m为常数,m>0)上任一点,将抛物线绕顶点G逆时针旋转90°后得到的新图象与y轴交于A、B两点(点A在点B的上方),点Q为点P旋转后的对应点.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
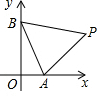 如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是
如图,点P在第一象限,△ABP是边长为2的等边三角形,当点A在x轴的正半轴上运动时,点B随之在y轴的正半轴上运动,运动过程中,点P到原点的最大距离是| 2 |
查看答案和解析>>
科目:初中数学 来源:2011年4月浙江省宁波市中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2010年江苏省无锡市天一实验学校中考数学三模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com