
| A. | 面积为3的正方形的长 | B. | 长为3,宽为2的长方形的对角线长 | ||
| C. | 体积为8的正方体的棱长 | D. | 对角线分别为2、4的菱形边长 |
分析 逐一算出每一个小题的数据,利用实数的意义判断即可.
解答 解:A、面积为3的正方形的边长为$\sqrt{3}$,是无理数,此选项错误;
B、长为3,宽为2的长方形的对角线长为$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$,是无理数,此选项错误;
C、体积为8的正方体的棱长为$\root{3}{8}$=2,是有理数,此选项正确;
D、对角线分别为2、4的菱形边长为$\sqrt{{(2÷2)}^{2}+(4÷2)^{2}}$=$\sqrt{5}$,是无理数,此选项错误.
故选:C.
点评 此题主要考查了实数的定义.有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:选择题
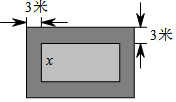 一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:
一标志性建筑的底面呈长方形,长是宽的2倍,在其四周铺上花岗岩,形成一个边宽为3米的长方形框(如图所示).已知铺这个框恰好用了504块边长为0.5米的正方向花岗岩(接缝忽略不计).若设此标志性建筑底面长方形的宽为x米,给出下列方程:| A. | ② | B. | ③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 关于x轴对称 | B. | 关于y轴对称 | ||
| C. | 关于直线x=-1对称 | D. | 关于直线y=-1对称 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
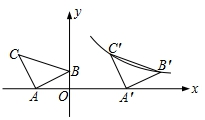 如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).
如图,在平面直角坐标系中有Rt△ABC,已知∠CAB=90°,AB=AC,A(-2,0),B(0,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
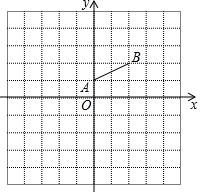 如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.
如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在格线上.线段AB的两个端点也在格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
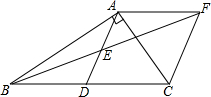 如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.
如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于F,连接CF,求证:四边形ADCF是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com