练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

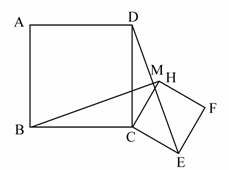
    在平面内正方形ABCD与正方形CEFH如图放置，连DE，BH，两线交于M.

    求证：（1）（4分）BH=DE.

    （2）（4分）BH⊥DE.

    　


    （1）证明△BCH△DCE，则 BH=DE                     …………………       5′

    （2）设CD与BH相交于G，则∠MBC+∠CGB=90°

      又 ∵∠CDE=∠MBC, ∠DGH=∠BGC

         ∵∠CDE+∠DGH=90°

         ∴∠GMD=90°

         ∴DE⊥BH                                    ……………            8′

    　

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    准备一张矩形纸片，按如图操作：

    将△ABE沿BE翻折，使点A落在对角线BD上的M点，将△CDF沿DF翻折，使点C落在对角线BD上的N点．

    （1）求证：四边形BFDE是平行四边形；

    （2）若四边形BFDE是菱形，AB=2，求菱形BFDE的面积．

     

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    ﹣的相反数是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    圆锥体的底面半径为2，侧面积为8，则其侧面展开图的圆心角为（   ） 

           A．90°             B.120°      C.150°      D.180°                 

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，直线过A(－1，2)、B(－2，0)两点，则的解集为              .

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：

    x(天)

    1

    2

    3

    …

    50

    p(件)

    118

    116

    114

    …

    20

    销售单价q(元/件)与x满足:当.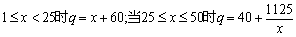

    （1）（2分）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系.

    （2）（4分）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式.

    （3）（4分）这50天中，该超市第几天获得利润最大？最大利润为多少？

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若y=(a+1)xa2-2是反比例函数，则a的取值为（　　）

    A．1                            B．-l                            C．±l                           D．任意实数

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在等腰梯形ABCD中，AD∥BC，AB=DC=50，AD=75，BC=135．点P从点B出发沿折线段BA﹣AD以每秒5个单位长的速度向点D匀速运动；点Q从点C出发沿线段CB方向以每秒3个单位长的速度向点B匀速运动；点P、Q同时出发，当点P与点D重合时停止运动，点Q也随之停止，设点P的运动时间为t秒．

    （1）点P到达点A、D的时间分别为　_________　秒和　_________　秒；

    （2）当点P在BA边上运动时，过点P作PN∥BC交DC于点N，作PM⊥BC，垂足为M，连接NQ，已知△PBM与△NCQ全等．

    ①试判断：四边形PMQN是什么样的特殊四边形？答：　_________　；

    ②若PN=3PM，求t的值；

    （3）当点P在AD边上运动时，是否存在PQ=DC？若存在，请求出t的值；若不存在，请说明理由．

     

     

     

     

     

     

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


     若不等式组 无解，则实数a的取值范围是(      )

    A．a≥一1    B．a<-1    C．a≤1   D.a≤-1

    查看答案和解析>>

    同步练习册答案