
【题目】如图,已知△ABC、△DEF都是正三角形,
(1)写出图中与∠AGF必定相等的角.
(2)对于(1)中的几个角,请你选择一个角证明与∠AGF相等(本小题将按照证明难度的大小分别给分,难度越大给分越多).
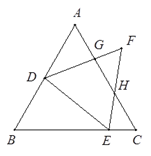
【答案】(1)∠DGH、∠ADE、∠BEH;(2)证明见试题解析.
【解析】试题分析:(1)易证∠AGF=∠F+∠FHG=60°+∠FHG,60°+∠FHG=∠C+∠EHC=∠BEH,得到∠AGF=∠BEH;由对顶角相等,得到∠DGH=∠AGF;在△ADG中,∠AGF=∠A+∠ADG=60°+∠ADG=∠EDG+∠ADG=∠ADE;
(2)由(1)的分析可得到证明过程.
试题解析:(1)∠DGH、∠ADE、∠BEH;
(2)证明∠AGF=∠DGH,∠AGF=∠ADE,∠AGF=∠BEH分别给1分,3分,5分.
①证明∠AGF=∠DGH,由对顶角相等,得到∠DGH=∠AGF;
②证明∠AGF=∠ADE,在△ADG中,∠AGF=∠A+∠ADG=60°+∠ADG=∠EDG+∠ADG=∠ADE,∴∠AGF=∠ADE;
③证明∠AGF=∠BEH,∵△ABC、△DEF均为正三角形,∴∠F=60°=∠C,∴∠AGF=∠F+∠GHF="∠C+" CHE=∠BEH.


科目:初中数学 来源: 题型:
【题目】计算或化简:
(1)2(a 4)3+a14÷a2—a2·a10 (2)(—2009)0+(![]() )—1+(—2)3
)—1+(—2)3
(3)(x-1)2+(2x+5)(5-2x) (4)(a+3b-2c)(a-3b-2c)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.
(1)求证:△ABQ≌△CAP;
(2)当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说明理由;若不变,求出它的度数.
(3)如图2,若点P、Q在运动到终点后继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC变化吗?若变化,请说明理由;若不变,则求出它的度数.
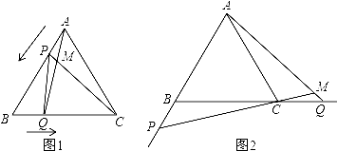
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点A(2,0),B(6,2),C(6,6),反比例函数y1=![]() (x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
(x>0)的图象过点D,点P是一次函数y2=kx+3-3k(k≠0)的图象与该反比例函数的一个公共点,对于下面四个结论:
①反比例函数的解析式是y1=![]() ;
;
②一次函数y2=kx+3-3k(k≠0)的图象一定经过(6,6)点;
③若一次函数y2=kx+3-3k的图象经过点C,当x>![]() 时,y1<y2;
时,y1<y2;
④对于一次函数y2=kx+3-3k(k≠0),当y随x的增大而增大时,点P横坐标a的取值范围是![]() <a<3.
<a<3.
其中正确的是( )
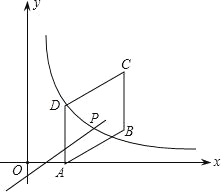
A.①③ B.②③ C.②④ D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小刚身高1.72m,他站立在阳光下的影子长为0.86m,紧接着他把手臂竖直举
起,影子长为1.15m,那么小刚举起的手臂超出头顶是_________m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=40°.
(1)作边AB的垂直平分线MN(保留作图痕迹,不写作法);
(2)在已作的图中,若MN交AC于点D,连结BD,求∠DBC的度数。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-x)·x3·x6=_________;
(2)(-b)4·(-b)5·(-b)=______;
(3)-22·(-2)2·(-2)3=____;
(4)(x-y)2·(y-x)4·(y-x)3=__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com