
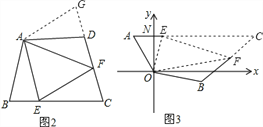
【题目】如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD上的点.且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G,使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是 ;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E、F分别是BC、CD上的点,且∠EAF=![]() ∠BAD,上述结论是否仍然成立,并说明理由;
∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离?
【答案】问题背景:EF=BE+DF;
探索延伸:EF=BE+DF仍然成立,理由见解析;
实际应用:此时两舰艇之间的距离是210海里.
【解析】解:问题背景:EF=BE+DF;
探索延伸:EF=BE+DF仍然成立.
证明如下:如图,延长FD到G,使DG=BE,连接AG,
∵∠B+∠ADC=180°,∠ADC+∠ADG=180°,∴∠B=∠ADG,
在△ABE和△ADG中,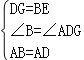 ,∴△ABE≌△ADG(SAS),
,∴△ABE≌△ADG(SAS),
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=∠BAD,
∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF,∴∠EAF=∠GAF,
在△AEF和△GAF中,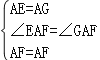 ,∴△AEF≌△GAF(SAS),∴EF=FG,
,∴△AEF≌△GAF(SAS),∴EF=FG,
∵FG=DG+DF=BE+DF,∴EF=BE+DF;
实际应用:如图,连接EF,延长AE、BF相交于点C,
∵∠AOB=30°+90°+(90°-70°)=140°,∠EOF=70°,∴∠EAF=∠AOB,
又∵OA=OB,∠OAC+∠OBC=(90°-30°)+(70°+50°)=180°,∴符合探索延伸中的条件,
∴结论EF=AE+BF成立,即EF=1.5×(60+80)=210海里.
答:此时两舰艇之间的距离是210海里.


科目:初中数学 来源: 题型:
【题目】甲经销商库存有1200套A品牌服装,每套进价400元,每套售价500元,一年内可卖完.现市场上流行B品牌服装,每套进价300元,每套售价600元,但一年内只允许经销商一次性订购B品牌服装,一年内B品牌服装销售无积压.因甲经销商无流动资金,只有低价转让A品牌服装,用转让来的资金购进B品牌服装,并销售.经与乙经销商协商,甲、乙双方达成转让协议,转让价格y(元/套)与转让数量x(套)之间的函数关系式为y=![]() .若甲经销商转让x套A品牌服装,一年内所获总利润为w(元).
.若甲经销商转让x套A品牌服装,一年内所获总利润为w(元).
(1)求转让后剩余的A品牌服装的销售款Q1(元)与x(套)之间的函数关系式;
(2)求B品牌服装的销售款Q2(元)与x(套)之间的函数关系式;
(3)求w(元)与x(套)之间的函数关系式,并求w的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班数学学习小组某次测验成绩分别是63,72,70,49,66,81,53,92,69,则这组数据的极差是( )
A. 47 B. 43 C. 34 D. 29
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题唐代大诗人李白喜好饮酒作诗,民间有“李白斗酒诗百篇”之说.《算法统宗》中记载了一个“李白沽酒”的故事.诗云:
注:古代一斗是10升.
大意是:李白在郊外春游时,做出这样一条约定:遇 见朋友,先到酒店里将壶里的酒增加一倍,再喝掉其中的19升酒.按照这样的约定,在第3个店里遇到朋友正好喝光了壶中的酒.
(1)列方程求壶中原有多少升酒;
(2)设壶中原有a0升酒,在第n个店饮酒后壶中余an升酒,如第一次饮后所余酒为a1=2a0﹣19(升),第二次饮后所余酒为a2=2a1﹣19=2(2a0﹣19)﹣19=22a0﹣(21+1)×19(升),….
①用an﹣1的表达式表示an , 再用a0和n的表达式表示an;
②按照这个约定,如果在第4个店喝光了壶中酒,请借助①中的结论求壶中原有多少升酒.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD⊥BC,EF垂直平分AC,交AC于点F,交BC于点E,且BD=DE.
⑴若∠BAE=40°,求∠C的度数;
⑵若△ABC周长13cm,AC=6cm,求DC长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,∠BAC=45°,AB=BC.
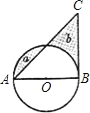
(1)求证:BC是⊙O的切线;
(2)设阴影部分的面积为a,b,⊙O的面积为S,请写出S与a,b的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过点C的切线互相垂直,垂足为D.
(1)求证:AC平分∠DAB;
(2)若sin∠ABC=![]() ,求tan∠BDC的值.
,求tan∠BDC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com