
����Ŀ��С����紴ҵ������һ��������Ϊ4Ԫ/ǧ�˵�ˮ��Ʒ�������г����鷢�֣�����ˮ��Ʒ����������y����ǧ�ˣ����ۼ�x��Ԫ/ǧ�ˣ�֮��Ĺ�ϵ��ͼ��ʾ��
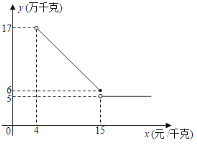
��1��������۴���ˮ��Ʒ����������y���ۼ�x֮��ĺ�������ʽ��
��2���г����黹���֣����۴���ˮ��Ʒ��Ҫ��Ͷ��ɱ�10��Ԫ�������������۹�������ˮ��Ʒ�����ʽ𣩣�����г��������Ź涨����ˮ��Ʒ�����ۼ۲�����20Ԫ/ǧ�ˣ������۴���ˮ��Ʒ�ۼ�Ϊ����Ԫʱ����õ��������������������Ƕ��٣�
���𰸡���1��y��![]() ����2�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ
����2�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ
��������
��1����4��x��15ʱ���躯������ʽΪy��kx+b������4��17������15��6�����뼴���������ʽ����x��15ʱ��y��5�����ɵõ��𰸣�
��2�����õ�������Ϊw��Ԫ���������������4��x��15ʱ���е�w����x��4������x+21����10������x��12.5��2+62.25�����ݺ��������ʵõ���x��12.5ʱ��w�����ֵΪ62.25��Ԫ����15��x��20ʱ���е�w����x��4����5��10��5x��30������һ�κ��������ʵõ���x��20ʱ��w�����ֵ��Ϊ70��Ԫ�����߱Ƚϼ��ɵõ�����
�⣺��1����4��x��15ʱ���躯������ʽΪy��kx+b������4��17������15��6������ã�
![]() ��
��
��ã�![]() ��
��
��y����x+21��
��x��15ʱ��y��5��
����������y���ۼ�x֮��ĺ�������ʽΪ��y��![]() .
.
��2�����õ�������Ϊw��Ԫ����������ã�
��4��x��15ʱ��
w����x��4������x+21����10
������x��12.5��2+62.25��
�߶�����ϵ��Ϊ��1��0��
�൱x��12.5ʱ��w�����ֵ��Ϊ62.25��Ԫ��
��15��x��20ʱ��
w����x��4����5��10��5x��30��
�൱x��20ʱ��w�����ֵ��Ϊ70��Ԫ��
��70��62.25��
�����۴���ˮ��Ʒ�ۼ�Ϊ20Ԫʱ����õ���������������������70��Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��4��0����B��0��![]() ������һ��ֱ�����dz�DEF������OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»�����������EFD=30����ED=2����GΪ��FD���е㣮
������һ��ֱ�����dz�DEF������OAB�ڣ�ʹ��б��FD���߶�AB�ϣ����dz߿������߶�AB���»�����������EFD=30����ED=2����GΪ��FD���е㣮

��1����ֱ��AB�Ľ���ʽ��
��2����ͼ1������D���A�غ�ʱ������G�ķ���������![]() ��
��![]() ���Ľ���ʽ��
���Ľ���ʽ��
��3�������dz����Ĺ����У�������G�ķ�����������ͼ���ܷ�ͬʱ������F������ܣ������ʱ�����������Ľ���ʽ��������ܣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�� ������![]() ��
��![]() �ύ�ڵ�A��-1,0�����������꣨1��n����
�ύ�ڵ�A��-1,0�����������꣨1��n����![]() ��Ľ����ڣ�0,2������0,3��֮�䣨�� ���˵㣩�������н��ۣ���
��Ľ����ڣ�0,2������0,3��֮�䣨�� ���˵㣩�������н��ۣ���![]() ����
����![]() ���۶�������ʵ��m��
���۶�������ʵ��m��![]() �ܳ������ܹ���
�ܳ������ܹ���![]() �ķ���
�ķ���![]() ����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ
����������ȵ�ʵ���������н�����ȷ�ĸ���Ϊ![]() ����
����![]()

A. 1 �� B. 2 �� C. 3 �� D. 4 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
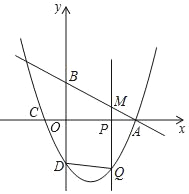
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y����![]() x+2�ֱ�x�ᡢy���ڵ�A��B����C�������ǣ���1��0����������y��ax2+bx��2����A��C�����ҽ�y���ڵ�D����PΪx����һ�㣬����P��x��Ĵ��߽�ֱ��AB�ڵ�M�����������ڵ�Q������DQ�����P�ĺ�����Ϊm��m��0����
x+2�ֱ�x�ᡢy���ڵ�A��B����C�������ǣ���1��0����������y��ax2+bx��2����A��C�����ҽ�y���ڵ�D����PΪx����һ�㣬����P��x��Ĵ��߽�ֱ��AB�ڵ�M�����������ڵ�Q������DQ�����P�ĺ�����Ϊm��m��0����
��1�����A�����꣮
��2���������ߵı���ʽ��
��3������B��D��Q��MΪ������ı�����ƽ���ı���ʱ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����λ���ȵ�С��������ɵ�12��12�����н���ƽ��ֱ������ϵ�������ABC�������������ߵĽ��㣩������ֱ���A����2��2����B����3��1����C����1��0����
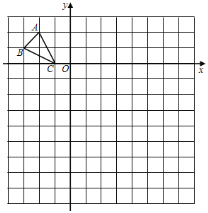
��1������ABC������ƽ��2����λ���ȣ�����ƽ��7����λ���ȣ��õ���DEF��������DEF��
��2����OΪλ�����ģ�����ABC�Ŵ�Ϊԭ����2�����������ڻ����Ŵ�����A1B1C1����P��x��y��Ϊ��ABC�е�����һ�㣬���Ӧ��P1������Ϊ�� ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ӿ��һ������������ϲ���������˶�,ij��ѧΪ�˼�ǿѧ������Ӿ��ȫ��ʶ����֯ѧ���ۿ��˼�ʵƬ���������벻Ҫ˽����ˮ�������ڹۿ����ڱ�У��![]() ��ѧ�������˳������飮����������������������ͳ��ͼ�������������ͳ��ͼ�ش���������:
��ѧ�������˳������飮����������������������ͳ��ͼ�������������ͳ��ͼ�ش���������:

(I)��γ���������,�������� ��ѧ����
(2)��ȫ����ͳ��ͼ��
(3)���ݳ�������Ľ���������У![]() ��ѧ���д�Լ�ж����������ʱ���º�ѧ��Ӿ��?
��ѧ���д�Լ�ж����������ʱ���º�ѧ��Ӿ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB��AC����ACΪֱ���ġ�O��BC�ڵ�D����EΪAC�ӳ�����һ�㣬��DE�ǡ�O�����ߣ�
��1����֤����CDE��![]() ��BAC��
��BAC��
��2����AB��3BD��CE��4�����O�İ뾶��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�٣�ij�½���վվǰ�㳡��Ҫ�̻������Ϊ35000![]() ��ʩ�������̻���11000
��ʩ�������̻���11000![]() ��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣�
��ÿ��Ĺ���������Ϊԭ����1.5���������ǰ4������˸����̻����̣�
��1�������̻�����ԭ�ƻ�ÿ����ɶ���ƽ���ף�
��2�������̻���������һ�鳤Ϊ20![]() ����Ϊ8
����Ϊ8![]() �ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56
�ľ��οյأ��ƻ���������������ͬ�ľ����̵أ����ǵ����֮��Ϊ56![]() �������̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ����ʾ����������ͨ���Ŀ����Ƕ����ף�
�������̵�֮�估�ܱ����п�����ȵ�����ͨ������ͼ����ʾ����������ͨ���Ŀ����Ƕ����ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���EΪ�Խ���AC��һ�㣬��AE![]() CB������DE���ӳ���BC�ڵ�G������A��AH��BE�ڵ�H����BC�ڵ�F�����½��ۣ���BH
CB������DE���ӳ���BC�ڵ�G������A��AH��BE�ڵ�H����BC�ڵ�F�����½��ۣ���BH![]() HE���ڡ�BEG
HE���ڡ�BEG![]() 45�����ۡ�ABF �ա�DCG�� ��4BH2
45�����ۡ�ABF �ա�DCG�� ��4BH2![]() BG��CD��������ȷ���۵ĸ�����( )
BG��CD��������ȷ���۵ĸ�����( )
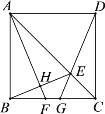
A.1��B.2
C.3D.4
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com