
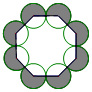
 如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )
如图,把八个等圆按相邻两两外切摆放,其圆心连线构成一个正八边形,设正八边形内侧八个扇形(无阴影部分)面积之和为S1,正八边形外侧八个扇形(有阴影部分)面积之和为S2,则$\frac{{S}_{1}}{{S}_{2}}$=( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | 1 |
科目:初中数学 来源: 题型:解答题
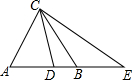 如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.
如图,△ABC中,AB=AC=8,D在AB上,E在AB的延长线上,∠ECB=∠DCB,AE=12.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
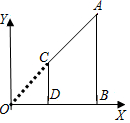 如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),
如图,AB,CD都垂直于x轴,垂足分别为B,D,若A(6,3),C(2,1),| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 1:8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.
如果点M、N在数轴上分别表示实数m,n,在数轴上M,N两点之间的距离表示为MN=m-n(m>n)或n-m(m<n)或|m-n|.利用数形结合思想解决下列问题:已知数轴上点A与点B的距离为16个单位长度,点A在原点的左侧,到原点的距离为26个单位长度,点B在点A的右侧,点C表示的数与点B表示的数互为相反数,动点P从A出发,以每秒1个单位的速度向终点C移动,设移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
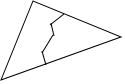 小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )
小丽不小心打碎了一块玻璃(如图),玻璃店老板根据涂总阴影部分重新划出一块与原来的玻璃完全相同的玻璃,其根据是( )| A. | SAS | B. | SSS | C. | ASA | D. | AAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,AD=2,CD=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
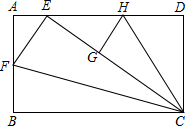 如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.
如图矩形ABCD是一张标准纸,长BC=AD=$\sqrt{2}$,AB=CD=1,把△BCF沿CF对折使点B恰好落在边AD上的点E处,再把△DCH沿CH对折使点D落在线段CE上的点G处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com