
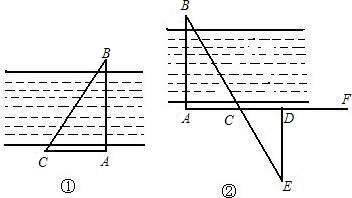
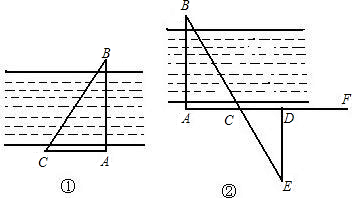
 解:方案1:
解:方案1: m.
m. m.
m.

 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

| 分割次数(n) | 1 | 2 | 3 | … | ||
| 一个最小等边三角形的面积(S) |
|
… |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•平谷区二模)在数学活动课上,老师请同学们在一张长为18cm,宽为14cm的长方形纸上剪下一个腰为12cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).小明同学按老师要求画出了如图的设计方案示意图,请你画出与小明的设计方案不同的所有满足老师要求的示意图,并通过计算说明哪种情况下剪下的等腰三角形的面积最小(含小明的设计方案示意图).
(2012•平谷区二模)在数学活动课上,老师请同学们在一张长为18cm,宽为14cm的长方形纸上剪下一个腰为12cm的等腰三角形(要求等腰三角形的一个顶点与长方形的一个顶点重合,其余两个顶点在长方形的边上).小明同学按老师要求画出了如图的设计方案示意图,请你画出与小明的设计方案不同的所有满足老师要求的示意图,并通过计算说明哪种情况下剪下的等腰三角形的面积最小(含小明的设计方案示意图).查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 5 |
| 29 |
| 34 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com