
 已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )
已知:如图在直角坐标系中,有菱形OABC,A点的坐标为(10,0),对角线OB、AC相交于D点,双曲线y=$\frac{k}{x}$(x>0)经过D点,交BC的延长线于E点,且OB•AC=160,则点E的坐标为( )| A. | (5,8) | B. | (5,10) | C. | (4,8) | D. | (3,10) |
分析 过点C作CF⊥x轴于点F,由OB•AC=160可求出菱形的面积,由A点的坐标为(10,0)可求出CF的长,由勾股定理可求出OF的长,故可得出C点坐标,对角线OB、AC相交于D点可求出D点坐标,用待定系数法可求出双曲线y=$\frac{k}{x}$(x>0)的解析式,由反比例函数的解析式与直线BC的解析式联立即可求出E点坐标即可.
解答  解:过点C作CF⊥x轴于点F,
解:过点C作CF⊥x轴于点F,
∵OB•AC=160,A点的坐标为(10,0),
∴OA•CF=$\frac{1}{2}$OB•AC=$\frac{1}{2}$×160=80,菱形OABC的边长为10,
∴CF=$\frac{80}{OA}$=$\frac{80}{10}$=8,
在Rt△OCF中,
∵OC=10,CF=8,
∴OF=$\sqrt{O{C}^{2}-C{F}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴C(6,8),
∵点D是线段AC的中点,
∴D点坐标为($\frac{10+6}{2}$,$\frac{8}{2}$),即(8,4),
∵双曲线y=$\frac{k}{x}$(x>0)经过D点,
∴4=$\frac{k}{8}$,即k=32,
∴双曲线的解析式为:y=$\frac{32}{x}$(x>0),
∵CF=8,
∴直线CB的解析式为y=8,
∴$\left\{\begin{array}{l}{y=\frac{32}{x}}\\{y=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=4}\\{y=8}\end{array}\right.$,
∴E点坐标为(4,8).
点评 此题考查了反比例函数图象上点的坐标特征,菱形的性质,以及勾股定理,熟练掌握性质及定理是解本题的关键.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:初中数学 来源: 题型:选择题
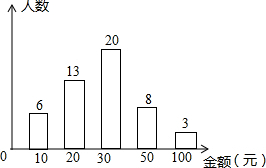 随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )
随着智能手机的普及,抢微信红包成为了春节期间人们最喜欢的活动之一.某中学九年级五班班长对全班50名学生在春节期间所抢的红包金额进行统计,并绘制成了统计图.根据如图提供的信息,红包金额的众数和中位数分别是( )| A. | 20、20 | B. | 30、20 | C. | 30、30 | D. | 20、30 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
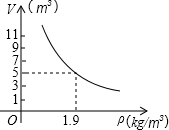 一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ=5kg/m3.
一定质量的二氧化碳,其体积V(m3)是密度ρ(kg/m3)的反比例函数,请你根据图中的已知条件,写出反比例函数的关系式,当V=1.9m3时,ρ=5kg/m3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月用水量 | 不超过12m3的部分 | 超过12m3的部分不超过18m3的部分 | 超过18m3的部分 |
| 收费标准(元/m3) | 2 | 2.5 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种图书 | 乙种图书 | |
| 进价(元/本) | 16 | 28 |
| 售价(元/本) | 26 | 40 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
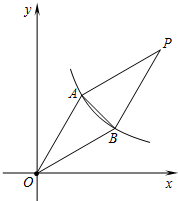 已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).
已知:如图,双曲线y=$\frac{k}{x}$在第一象限的分支经过A、B两点,点A的坐标为(2,2$\sqrt{3}$),点B的坐标为(m,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com