
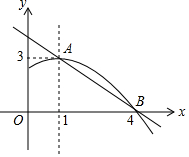
 如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:
如图是抛物线y1=ax2+bx+c(a≠0)的图象的一部分,抛物线的顶点坐标是A(1,3),与x轴的一个交点是B(4,0),直线y2=mx+n(m≠0)与抛物线交于A,B两点,下列结论:分析 根据二次函数的性质、方程与二次函数的关系、函数与不等式的关系一一判断即可.
解答 解:由图象可知:a<0,b>0,c>0,故abc<0,故①错误.
观察图象可知,抛物线与直线y=3只有一个交点,故方程ax2+bx+c=3有两个相等的实数根,故②正确.
根据对称性可知抛物线与x轴的另一个交点是(-2,0),故③错误,
观察图象可知,当1<x<4时,有y2<y1,故④错误,
因为x=1时,y1有最大值,所以ax2+bx+c≤a+b+c,即x(ax+b)≤a+b,故⑤正确,
所以②⑤正确,
故答案为②⑤.
点评 本题考查二次函数的性质、方程与二次函数的关系、函数与不等式的关系等知识,解题的关键是灵活运用所学知识解决问题,学会利用函数图象解决问题,所以中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:
荆州市某水产养殖户进行小龙虾养殖.已知每千克小龙虾养殖成本为6元,在整个销售旺季的80天里,销售单价p(元/千克)与时间第t(天)之间的函数关系为:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )
如图,在?ABCD中,对角线AC,BD相交于点O,添加下列条件不能判定?ABCD是菱形的只有( )| A. | AC⊥BD | B. | AB=BC | C. | AC=BD | D. | ∠1=∠2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com