
ЁОЬтФПЁПНЋвЛИБжБНЧШ§НЧАхШчЭМЂйАкЗХЃЌФмЙЛЗЂЯжЕШбќжБНЧШ§НЧАхABCЕФаББпгыКЌ30ЁуНЧЕФжБНЧШ§НЧАхDEFЕФГЄжБНЧБпDEжиКЯЃЌDF=8ЃЎ
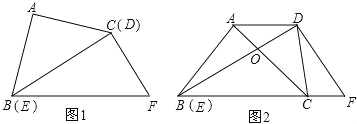
ЃЈ1ЃЉШєPЪЧBCЩЯЕФвЛИіЖЏЕуЃЌЕБPA=DFЪБЃЌЧѓДЫЪБЁЯPABЕФЖШЪ§ЃЛ
ЃЈ2ЃЉНЋЭМЂйжаЕФЕШбќжБНЧШ§НЧАхABCШЦЕуBЫГЪБеыа§зЊ30ЁуЃЌЕуCТфдкBFЩЯЃЌACгыBDНЛгкЕуOЃЌСЌНгCDЃЌШчЭМЂкЃЎ
ЂйЬНЧѓЁїCDOЕФаЮзДЃЌВЂЫЕУїРэгЩЃЛ
ЂкдкЭМЂйжаЃЌШєPЪЧBCЕФжаЕуЃЌСЌНгFPЃЌНЋЕШбќжБНЧШ§НЧАхABCШЦЕуBЫГЪБеыа§зЊЃЌЕБа§зЊНЧІС= ЪБЃЌFPГЄЖШзюДѓЃЌзюДѓжЕЮЊ ЃЈжБНгаДГіД№АИМДПЩЃЉЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ2ЃЉЂйМћЯъНтЃЛЂк
ЃЛЃЈ2ЃЉЂйМћЯъНтЃЛЂк![]() ЃЌ
ЃЌ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉзї![]() НЛBCгкЕуHЃЌгЩЕШбќШ§НЧаЮШ§ЯпКЯвЛМАжБНЧШ§НЧаЮаББпжаЯпЕФаджЪПЩЕУ
НЛBCгкЕуHЃЌгЩЕШбќШ§НЧаЮШ§ЯпКЯвЛМАжБНЧШ§НЧаЮаББпжаЯпЕФаджЪПЩЕУ![]() ЃЌдк
ЃЌдк![]() жаНтжБНЧШ§НЧаЮПЩжЊBCГЄЃЌМДжЊAHГЄЃЌЃЌдк
жаНтжБНЧШ§НЧаЮПЩжЊBCГЄЃЌМДжЊAHГЄЃЌЃЌдк![]() жаНтжБНЧШ§НЧаЮПЩжЊ
жаНтжБНЧШ§НЧаЮПЩжЊ![]() ЃЌЗжЕуPдк
ЃЌЗжЕуPдк![]() ЮЛжУКЭдк
ЮЛжУКЭдк![]() ЮЛжУ2жжЧщПіЧѓНтМДПЩЃЛ
ЮЛжУ2жжЧщПіЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЂйРћгУЕШбќШ§НЧаЮСНЕзНЧЯрЕШМАШ§НЧаЮЭтНЧЕФаджЪПЩЧѓЕУ![]() ЃЌвзжЊЁїCDOЮЊЕШбќШ§НЧаЮЃЛ
ЃЌвзжЊЁїCDOЮЊЕШбќШ§НЧаЮЃЛ
ЂкгЩЕуPЪЧBCЕФжаЕуЃЌFPГЄЖШзюДѓЃЌПЩжЊЕуFЁЂBЁЂPдкЭЌвЛЬѕжБЯпЩЯЃЌМДЕуPдкFBЕФбгГЄЯпЩЯЃЌвзжЊа§зЊНЧ![]() ЃЌЧѓГіBPЁЂBFЕФГЄЃЌЯрМгМДЮЊFPГЄ.
ЃЌЧѓГіBPЁЂBFЕФГЄЃЌЯрМгМДЮЊFPГЄ.
НтЃКЃЈ1ЃЉШчЭМЃЌзї![]() НЛBCгкЕуHЃЌ
НЛBCгкЕуHЃЌ

![]() ЮЊЕШбќжБНЧШ§НЧаЮ
ЮЊЕШбќжБНЧШ§НЧаЮ
![]()
![]()
![]()
![]()
![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]()
![]()
ЕБЕуPдк![]() ЮЛжУЪБЃЌ
ЮЛжУЪБЃЌ
![]() ЃЌ
ЃЌ![]()
![]() ЃЛ
ЃЛ
ЕБЕуPдк![]() ЮЛжУЪБЃЌ
ЮЛжУЪБЃЌ
![]() ЃЌ
ЃЌ![]()
![]()
![]()
![]()
злЩЯЫљЪіЃЌЁЯPABЕФЖШЪ§ЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЁїCDOЮЊЕШбќШ§НЧаЮ.
![]()
![]() ЃЌМД
ЃЌМД![]()
![]()
![]()
![]()
![]()
ЫљвдЁїCDOЮЊЕШбќШ§НЧаЮЃЛ
Ђк![]() ЕуPЪЧBCЕФжаЕуЃЌFPГЄЖШзюДѓЃЌдђЕуFЁЂBЁЂPдкЭЌвЛЬѕжБЯпЩЯЃЌМДЕуPдкFBЕФбгГЄЯпЩЯЃЌШчЭМЫљЪОЃЌ
ЕуPЪЧBCЕФжаЕуЃЌFPГЄЖШзюДѓЃЌдђЕуFЁЂBЁЂPдкЭЌвЛЬѕжБЯпЩЯЃЌМДЕуPдкFBЕФбгГЄЯпЩЯЃЌШчЭМЫљЪОЃЌ
![]() Бпа§зЊСЫ
Бпа§зЊСЫ![]()
![]()
![]()
![]() ЕуP
ЕуP![]()
![]()
дк![]() жаЃЌ
жаЃЌ
![]()
![]()
![]()
ЫљвдЕБа§зЊНЧ![]() ЪБЃЌFPГЄЖШзюДѓЃЌзюДѓжЕЮЊ
ЪБЃЌFPГЄЖШзюДѓЃЌзюДѓжЕЮЊ![]() .
.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
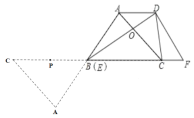
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌCЃЌGЪЧЁбOЩЯСНЕуЃЌЧв![]() ЃЌЙ§ЕуCЕФжБЯпCDЁЭBGгкЕуDЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌСЌНгBCЃЌНЛODгкЕуFЃЎ
ЃЌЙ§ЕуCЕФжБЯпCDЁЭBGгкЕуDЃЌНЛBAЕФбгГЄЯпгкЕуEЃЌСЌНгBCЃЌНЛODгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКCDЪЧЁбOЕФЧаЯпЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓжЄЃКAE=AOЃЛ
ЃЌЧѓжЄЃКAE=AOЃЛ
ЃЈ3ЃЉСЌНг ADЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєCD ![]() ЃЌЧѓADЕФГЄЃЎ
ЃЌЧѓADЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛЬѕХзЮяЯпгыxжсЯрНЛгкAЁЂBСНЕу(ЕуAдкЕуBЕФзѓВр)ЃЌЦфЖЅЕуPдкЯпЖЮMNЩЯвЦЖЏЃЎШєЕуMЁЂNЕФзјБъЗжБ№ЮЊ(-1ЃЌ-1)ЁЂ(2ЃЌ-1)ЃЌЕуBЕФКсзјБъЕФзюДѓжЕЮЊ3ЃЌдђЕуAЕФКсзјБъЕФзюаЁжЕЮЊ( )
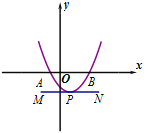
A.-3B.-2.5C.-2D.-1.5
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Љ4x+3ЃЎ
ЃЈ1ЃЉЧѓИУЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕуКЭЖдГЦжсЃЛ
ЃЈ2ЃЉдкЫљИјзјБъЯЕжаЛГіИУЖўДЮКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ3ЃЉИљОнЭМЯѓжБНгаДГіЗНГЬx2Љ4x+3ЃН0ЕФИљЃЛ
ЃЈ4ЃЉИљОнЭМЯѓаДГіЕБyЃМ0ЪБЃЌxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊе§ЗНаЮABCDЃЌЖдНЧЯпACЁЂBDНЛгкЕуOЃЌЯпЖЮOEЁЭOFЃЌЧвгыБпADЁЂABНЛгкЕуEЁЂFЃЎ
ЃЈ1ЃЉЧѓжЄЃКOEЃНOFЃЛ
ЃЈ2ЃЉСЌНгEFЃЌНЛACгкЕуHЃЌШєHFЃКAFЃН![]() ЃК2ЃЌЧѓOHЃКEFЃЛ
ЃК2ЃЌЧѓOHЃКEFЃЛ
ЃЈ3ЃЉШєEЁЂFЗжБ№дкDAЁЂABбгГЄЯпЩЯЃЌOEгыABНЛгкЕуMЃЌШєЁїMOFЁзЁїEAFЃЌAFЃН1ЃЌЧѓе§ЗНаЮABCDЕФБпГЄЃЎ
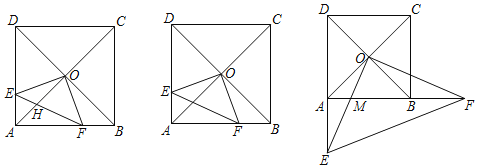
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌRtЁїABCжаЃЌЁЯC=90ЁуЃЎBEЦНЗжЁЯABCНЛACгкЕуDЃЌНЛЁїABCЕФЭтНгдВгкЕуEЃЌЙ§ЕуEзїEFЁЭBCНЛBCЕФбгГЄЯпгкЕуFЃЎЧыВЙШЋЭМаЮКѓЭъГЩЯТУцЕФЮЪЬтЃК
ЃЈ1ЃЉЧѓжЄЃКEFЪЧЁїABCЭтНгдВЕФЧаЯпЃЛ
ЃЈ2ЃЉШєBC=5ЃЌsinЁЯABC=![]() ЃЌЧѓEFЕФГЄЃЎ
ЃЌЧѓEFЕФГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЁї![]() жаЃЌ
жаЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() ЕНЕу
ЕНЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮBCEFЪЧСтаЮЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓСтаЮBCEFЕФУцЛ§ЃЎ
ЃЌЧѓСтаЮBCEFЕФУцЛ§ЃЎ
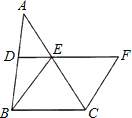
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаћКЭжабЇЭМЪщЙнНёШеЙКНјМзЁЂввСНжжЭМЪщЃЌУПБОМзжжЭМЪщЕФНјМлБШУПБОввжжЭМЪщЕФНјМлИп20дЊЃЌЛЈ780дЊЙКНјМзжжЭМЪщЕФЪ§СПгыЛЈ540дЊЙКНјввжжЭМЪщЕФЪ§СПЯрЭЌЃЎ
ЃЈ1ЃЉЧѓМзЁЂввСНжжЭМЪщУПБОЕФНјМлЗжБ№ЪЧЖрЩйдЊЃЛ
ЃЈ2ЃЉаћКЭжабЇЙКНјМзЁЂввСНжжЭМЪщЙВ70БОЃЌзмЙКЪщЗбгУВЛГЌЙ§3950дЊЃЌдђзюЖрЙКНјМзжжЭМЪщЖрЩйБОЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЧьзЃИФИяПЊЗХ40жмФъєпЮвАЎЮвМвУРРіЧрбђШКжкЮФвееЙбндВТњТфФЛЃЌФГбЇЯАаЁзщЖдЮФвееЙбнжаЕФAЮшЕИЁЖВЛЭќГѕаФЁЗЃЌBЖРЮшЁЖРцдАвЛЩњЁЗЃЌCЮшЕИЁЖьХЖЏЕФУЕЙхЁЗЃЌDГЏЯЪзщИшЮшЁЖАЂРяРЩ+atepЁЗетЫФИіНкФППЊеЙЁАЮвзюЯВАЎЕФЮшЕИНкФПЁБЕїВщЃЌЫцЛњЕїВщСЫВПЗжЙлжкЃЈУПЮЛЙлжкБибЁЧвжЛФмбЁетЫФИіНкФПжаЕФвЛИіЃЉВЂНЋЕУЕНЕФаХЯЂ
ЛцжЦСЫЯТУцСНЗљВЛЭъећЕФЭГМЦЭМЃК
ЃЈ1ЃЉБОДЮвЛЙВЕїВщСЫЖрЩйУћЙлжкЃЛВЂНЋЬѕаЮЭГМЦЭМВЙГфЭъећЃЛ
ЃЈ2ЃЉбЇЯАаЁзщзМБИДг4ИіНкФПжаЫцЛњбЁШЁСНИіНкФПЕФТМЯёДјЛибЇаЃИјЭЌбЇУЧЙлПДЃЌЧыгУЪїзДЭМЛђепСаБэЕФЗНЗЈЧѓЧЁКУбЁжаAЮшЕИЁЖВЛЭќГѕаФЁЗКЭCЮшЕИЁЖьХЖЏЕФУЕЙхЁЗЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com