
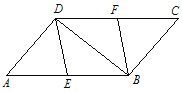
【题目】如图,在□ABCD 中,∠ADB=90°,点 E 为 AB 边的中点,点 F 为CD 边的中点.
(1)求证:四边形 DEBF 是菱形;
(2)当∠A 等于多少度时,四边形 DEBF 是正方形?并说明你的理由.
【答案】见解析
【解析】试题分析:(1)根据平行四边形的性质得出DC∥AB,DC=AB,求出DF∥BE,DF=BE,得出四边形DEBF是平行四边形,求出DE=BE,根据菱形的判定得出即可;
(2)求出AD=BD,根据等腰三角形的性质得出DE⊥AB,根据正方形的判定得出即可.
试题解析:(1)证明:∵四边形ABCD是平行四边形,∴DC∥AB,DC=AB.∵点E为AB边的中点,点F为CD边的中点,∴DF∥BE,DF=BE,∴四边形DEBF是平行四边形.∵∠ADB=90°,点E为AB边的中点,∴DE=BE=AE,∴四边形DEBF是菱形;
(2)当∠A=45°,四边形DEBF是正方形.理由如下:
∵∠ADB=90°,∠A=45°,∴∠A=∠ABD=45°,∴AD=BD.∵E为AB的中点,∴DE⊥AB,即∠DEB=90°.∵四边形DEBF是菱形,∴四边形DEBF是正方形.


科目:初中数学 来源: 题型:
【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
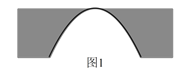
【题目】河上有一座桥孔为抛物线形的拱桥(如图 ![]() ),水面宽
),水面宽 ![]() 时,水面离桥孔顶部
时,水面离桥孔顶部 ![]() ,因降暴雨水面上升
,因降暴雨水面上升 ![]() .
.
(1)建立适当的坐标系,并求暴雨后水面的宽;(结果保留根号)
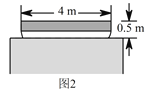
(2)一艘装满物资的小船,露出水面的部分高为 ![]() ,宽
,宽 ![]() (横断面如图
(横断面如图 ![]() 所示),暴雨后这艘船能从这座拱桥下通过吗?
所示),暴雨后这艘船能从这座拱桥下通过吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用火柴棒按下列方式搭建三角形:
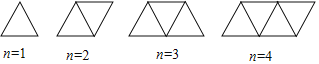
(1)当三角形个数为1时,需3根火柴棒;当三角形个数为2时,需5根火柴棒;则当三角形个数为100时,需火柴棒 根;当三角形个数为n时,需火柴棒 根(用含n的代数式表示);
(2)当火柴棒的根数为2019时,求三角形的个数?
(3)组成三角形的火柴棒能否为1000根,如果能,求三角形的个数;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
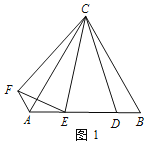
【题目】【操作发现】如图 1,△ABC 为等边三角形,点 D 为 AB 边上的一点,∠DCE=30°,将线段 CD 绕点 C 顺时针旋转 60°得到线段 CF,连接 AF、EF. 请直接 写出下列结果:
① ∠EAF的度数为__________;
② DE与EF之间的数量关系为__________;
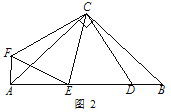
【类比探究】如图 2,△ABC 为等腰直角三角形,∠ACB=90°,点 D 为 AB 边上的一点∠DCE=45°,将线段 CD 绕点 C 顺时针旋转 90°得到线段 CF,连接 AF、EF.
①则∠EAF的度数为__________;
② 线段 AE,ED,DB 之间有什么数量关系?请说明理由;
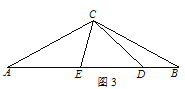
【实际应用】如图 3,△ABC 是一个三角形的余料.小张同学量得∠ACB=120°,AC=BC, 他在边 BC 上取了 D、E 两点,并量得∠BCD=15°、∠DCE=60°,这样 CD、CE 将△
ABC 分成三个小三角形,请求△BCD、△DCE、△ACE 这三个三角形的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华思考解决如下问题:
原题:如图1,点P,Q分别在菱形ABCD的边BC,CD上,∠PAQ=∠B,求证:AP=AQ.
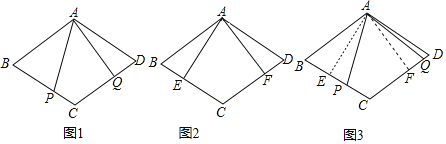
(1)小华进行探索,若将点P,Q的位置特殊化:把∠PAQ绕点A旋转得到∠EAF,使AE⊥BC,点E、F分别在边BC、CD上,如图2.此时她证明了AE=AF,请你证明;
(2)由以上(1)的启发,在原题中,添加辅助线:如图3,作AE⊥BC,AF⊥CD,垂足分别为E,F.请你继续完成原题的证明;
(3)如果在原题中添加条件:AB=4,∠B=60°,如图1,求四边形APCQ的周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
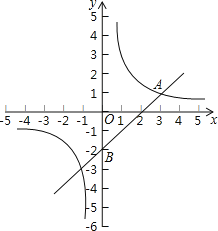
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com