
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
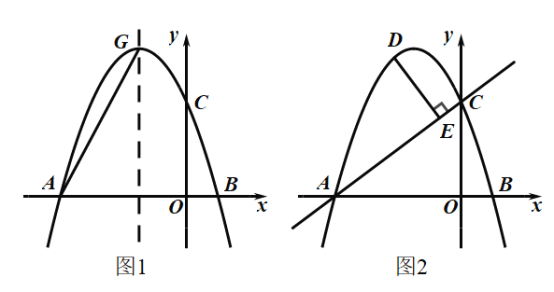
(1)求抛物线的解析式;
(2)如图1,抛物线的对称轴交抛物线于点![]() ,在
,在![]() 轴上是否存在点
轴上是否存在点![]() ,使得
,使得![]() 的周长最小?若存在,求出点
的周长最小?若存在,求出点![]() 坐标;若不存在,请说明理由;
坐标;若不存在,请说明理由;
(3)如图2,点![]() 为直线
为直线![]() 上方抛物线上的动点,
上方抛物线上的动点,![]() 于点
于点![]() ,求线段
,求线段![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)由题意利用待定系数法将![]() ,
,![]() 代入
代入![]() 求解即可;
求解即可;
(2)根据题意作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 的周长最小,并设直线
的周长最小,并设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() ,进行分析运算求解即可;
,进行分析运算求解即可;
(3)根据题意过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() ,进而求出点
,进而求出点![]() 的坐标并设直线
的坐标并设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]() 代入
代入![]() 进行运算以及设平行于
进行运算以及设平行于![]() 的直线为
的直线为![]() 进行分析运算.
进行分析运算.
解:(1)将![]() ,
,![]() 代入
代入![]() 得,
得, 解得,
解得,
∴抛物线的解析式为![]() .
.
(2)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,连接
,连接![]() ,交
,交![]() 轴于点
轴于点![]() ,此时
,此时![]() 的周长最小.
的周长最小.

![]()
![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,将
,将![]() ,
,![]()
代入![]() ,得
,得 ,
,
解得 ,
,
∴直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]()
∴点![]() 的坐标为
的坐标为![]() .
.
(3)如图,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 交
交![]() 于点
于点![]() .
.

当![]() 时,
时,![]()
∴点![]() 的坐标为
的坐标为![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
得![]()
解得 ,
,
∴直线![]() 的解析式为
的解析式为![]()
设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]()
![]()
设平行于![]() 的直线为
的直线为![]() ,
,
解方程组 ,
,
得![]()
由判别式![]() ,
,
得![]()
此时,直线![]() 与直线
与直线![]() 的距离即为
的距离即为![]() 的最大值.
的最大值.
求得,![]() .
.


科目:初中数学 来源: 题型:
【题目】天然生物制药公司投资制造某药品,先期投入了部分资金.企划部门根据以往经验发现,生产销售中所获总利润![]() 随天数
随天数![]() (可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到
(可以取分数)的变化图象如下,当总利润到达峰值后会逐渐下降,当利润下降到![]() 万元时即为止损点,则停止生产
万元时即为止损点,则停止生产
(1)设![]() ,求出最大利润是多少?
,求出最大利润是多少?
(2)在(1)的条件下,经公司研究发现如果添加![]() 名工人
名工人![]() ,在工资成本增加的情况下,总利润关系式变为
,在工资成本增加的情况下,总利润关系式变为![]() ,请研究添加
,请研究添加![]() 名工人后总利润的最大值,并给出总利润最大的方案中的
名工人后总利润的最大值,并给出总利润最大的方案中的![]() 值及生产天数.
值及生产天数.
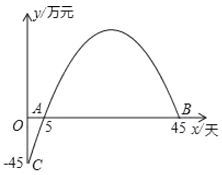
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明想利用所学知识测量一公园门前热气球直径的大小,如图,当热气球升到某一位置时,小明在点A处测得热气球底部点C、中部点D的仰角分别为50°和60°,已知点O为热气球中心,EA⊥AB,OB⊥AB,OB⊥OD,点C在OB上,AB=30m,且点E、A、B、O、D在同一平面内,根据以上提供的信息,求热气球的直径约为多少米?(精确到0.1m)
(参考数据:sin50°≈0.7660,cos50°≈0.6428,tan50°=1.192)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】通过学习锐角三角比,我们知道在直角三角形中,一个锐角的大小与两条边长的比值是一一对应的,因此,两条边长的比值与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做底角的邻对(can),如图(1)在△ABC中,AB=AC,底角B的邻对记作canB,这时canB=底边/腰=![]() ,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
,容易知道一个角的大小与这个角的邻对值也是一一对应的.根据上述角的邻对的定义,解下列问题:
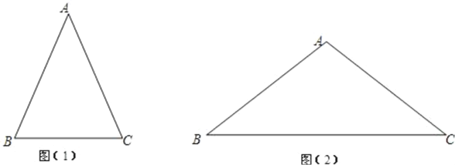
(1)can30°= ;
(2)如图(2),已知在△ABC中,AB=AC,canB=![]() ,S△ABC=24,求△ABC的周长.
,S△ABC=24,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=4,BO=DO=3,点P为线段AC上的一个动点.过点P分别作PM⊥AD于点M,作PN⊥DC于点N. 连接PB,在点P运动过程中,PM+PN+PB的最小值等于_________ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
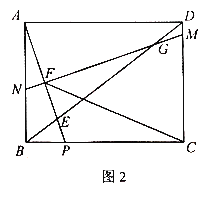
【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,![]() .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
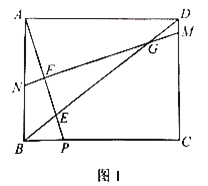
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() .
.
(3)如图2,在(2)的条件下,连接CF,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,反比例函数
,反比例函数![]() (a,b,k是常数,且
(a,b,k是常数,且![]() ),若其中一部分x,y的对应值如表:则不等式
),若其中一部分x,y的对应值如表:则不等式![]() 的解集是_________.
的解集是_________.
x |
|
|
|
| 1 | 2 | 3 | 4 |
| 3 | 2 | 1 | 0 |
|
|
|
|
|
| 2 | 3 | 6 |
|
|
|
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点E是AD的中点,连接CE,并延长CE与BA的延长线交于点F, 若∠BCF=90°,则∠D的度数为( )
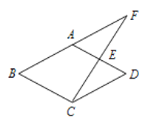
A.60°B.55°C.45°D.40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com