
【题目】完成下面的证明过程:
如图所示,直线AD与AB,CD分别相交于点A,D,与EC,BF分别相交于点H,G,已知∠1=∠2,∠B=∠C.
求证:∠A=∠D.
证明:∵∠1=∠2,(已知)∠2=∠AGB( )
∴∠1= ( )
∴EC∥BF( )
∴∠B=∠AEC( )
又∵∠B=∠C(已知)
∴∠AEC= ( )
∴ ( )
∴∠A=∠D( )

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】一盒中有x个黑球和2个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,黑球的概率是 ![]() .
.
(1)填空:x=;
(2)从该盒子中随机摸出一个球,记下颜色后,不放回,再从该盒子中摸出一个球记下颜色,请用画树状图或列表求两次摸出的球的颜色都是白色的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民节水意识,合理利用水资源,某市采用价格调控手段达到节约用水的目的,规定:每户居民每月用水不超过15m3时,按基本价格收费;超过15m3时,不超过的部分仍按基本价格收费,超过的部分要加价收费,该市某户居民今年4、5月份的用水量和水费如表所示:
月份 | 用水量/m3 | 水费/元 |
4 | 16 | 50 |
5 | 20 | 70 |
(1)求该市居民用水的两种收费价格;
(2)若该居民6月份交水费80元,那么该居民这个月水量为m3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,o为坐标原点,点A的坐标为(![]() ,3),点B的坐标(
,3),点B的坐标(![]() ,6).
,6).
(1)若AB与坐标轴平行,求AB的长;
(2)若![]() 满足
满足![]() AC⊥
AC⊥![]() 轴,垂足为C,BD⊥
轴,垂足为C,BD⊥![]() 轴,垂足为D:
轴,垂足为D:
①求四边形ACDB的面积;
②连AB、OA、OB,若△OAB的面积大于6而小于10,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3a经过点A(﹣1,0)、C(0,3),与x轴交于另一点B,抛物线的顶点为D.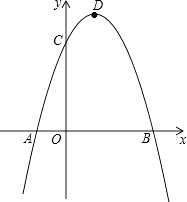
(1)求此二次函数解析式;
(2)连接DC、BC、DB,求证:△BCD是直角三角形;
(3)在对称轴右侧的抛物线上是否存在点P,使得△PDC为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC绕着点O按顺时针方向旋转90°后到达△CDE的位置,下列说法中不正确的是( )

A. AB⊥CD
B. AC⊥CE
C. BC⊥DE
D. 点C与点B是两个三角形的对应点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1=∠2,AC=AD,要使△ABC≌△AED,还需添加一个条件,那么在①AB=AE,②BC=ED,③∠C=∠D,④∠B=∠E,这四个关系中可以选择的是( )
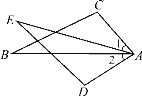
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:
材料一:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() 来表示
来表示![]() 的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:
的整数部分是1,将这个数减去其整数部分,差就是小数部分.由此我们得到一个真命题:
如果![]() ,其中
,其中![]() 是整数,且
是整数,且![]() 那么
那么![]() .
.
材料二:已知![]() 是有理数,并且满足等式
是有理数,并且满足等式![]() 求
求![]() 的值.
的值.
解:![]()
![]()
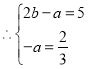 ,解得
,解得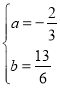
请解答:
(1)如果![]() ,其中
,其中![]() 是整数,且
是整数,且![]() 那么
那么![]() _______,
_______,![]() ______.
______.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值;
的值;
(3)已知![]() 是有理数,并且满足等式
是有理数,并且满足等式![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△CDE均为等边三角形,且点B,C,D在同一直线上,连结AD,BE,分别交CE和AC于点G,H,连结GH.
(1)请说出AD=BE的理由;
(2)试说出△BCH≌△ACG的理由;
(3)试猜想△CGH是什么特殊的三角形,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com