
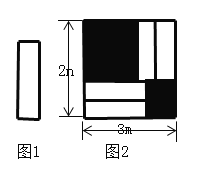
【题目】把四张形状大小完全相同的小长方形卡片(如图1)不重叠地放在一个底面为长方形(长为![]() 厘米,宽为
厘米,宽为![]() 厘米))的盒了底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是____________厘米
厘米))的盒了底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示,则图2中两块阴影部分的周长和是____________厘米
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,E为线段AB上的点,点D为线段AE的中点.
![]()
(1)若线段AB=a,CE=b,|a﹣17|+(b﹣5.5)2=0,求线段AB、CE的长;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=20,AD=2BE,求线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司经销甲种型号电脑,每台售价4000元.为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
(1)有几种进货方案?
(2)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少? 若考虑投入成本最低,则应选择哪种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
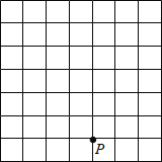
【题目】如图,网格中每个小正方形的边长均为1个单位长度,点P的坐标为(2,-2),请解答下列问题:
(1)将平面直角坐标系补充完整,并描出下列各点:A(-1,0),B(3,-1),C(4,3);
(2)顺次连接A,B,C,组成三角形ABC,求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是等边三角形,P为平面内的一个动点,BP=BA,0<∠PBC<180 ,DB平分∠PBC,且DB=DA.
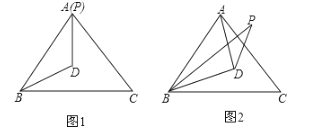
(1)当BP与BA重合时(如图1),求∠BPD的度数;
(2)当BP在∠ABC的内部时(如图2),求∠BPD的度数;
(3)当BP在∠ABC的外部时,请你直接写出∠BPD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面二孩政策于2016年1月1日正式实施,黔南州某中学对八年级部分学生进行了随机问卷调查,其中一个问题“你爸妈如果给你添一个弟弟(或妹妹),你的态度是什么?”共有如下四个选项(要求仅选择一个选项):
A.非常愿意 B.愿意 C.不愿意 D.无所谓
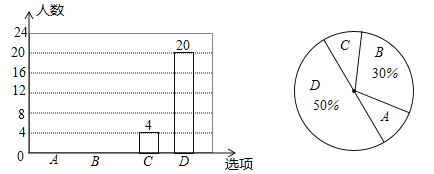
如图是根据调查结果绘制的两幅不完整的统计图,请结合图中信息解答以下问题:
(1)试问本次问卷调查一共调查了多少名学生?并补全条形统计图;
(2)若该年级共有450名学生,请你估计全年级可能有多少名学生支持(即态度为“非常愿意”和“愿意”)爸妈给自己添一个弟弟(或妹妹)?
(3)在年级活动课上,老师决定从本次调查回答“不愿意”的同学中随机选取2名同学来谈谈他们的想法,而本次调查回答“不愿意”的这些同学中只有一名男同学,请用画树状图或列表的方法求选取到两名同学中刚好有这位男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
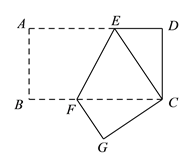
【题目】已知将一矩形纸片ABCD折叠,使顶点A与C重合,折痕为EF.
(1)求证:CE=CF;
(2)若AB =8 cm,BC=16 cm,连接AF,写出求四边形AFCE面积的思路.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E。
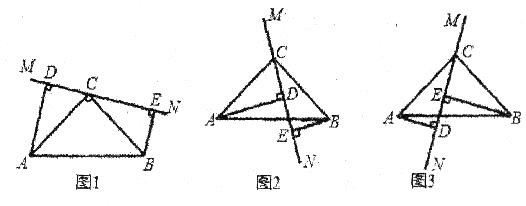
(1)①求证图1中△ADC≌△CEB;②证明DE=AD+BE;
(2)当直线MN绕点C旋转到图2的位置时,请说明DE=AD-BE的理由;
(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE又具有怎样的等量关系?请直接写出这个等量关系(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:
(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;
(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;
(3)连接BD,BC.
下列说法不正确的是( )

A. ∠CBD=30° B. S△BDC=![]() AB2
AB2
C. 点C是△ABD的外心 D. sin2A+cos2D=l
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com