
分析 (1)根据不等式的基本性质先去括号,然后通过移项、合并同类项即可求得原不等式的解集;
(2)根据(1)中的x的取值范围来确定x的最小整数解;然后将x的值代入已知方程列出关于系数a的一元一次方程2×(-2)-a×(-2)=3,通过解该方程求得a的值,再代入-a2+$\frac{29}{4}$计算即可.
解答 解:(1)5(x-2)+8<6(x-1)+7,
5x-10+8<6x-6+7,
5x-2<6x+1,
-x<3,
x>-3.
(2)由(1)得,最小整数解为x=-2,
∴2×(-2)-a×(-2)=3,
∴a=$\frac{7}{2}$,
∴-a2+$\frac{29}{4}$=-($\frac{7}{2}$)2+$\frac{29}{4}$=-5.
点评 本题考查了解一元一次不等式、一元一次方程的解,一元一次不等式的整数解以及代数式求值.解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
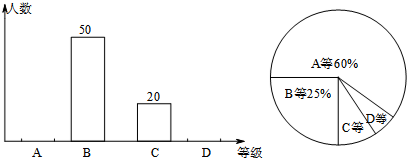
| A. | 样本容量是200 | |
| B. | 样本中C等所占百分比是10% | |
| C. | D等所在扇形的圆心角为15° | |
| D. | 估计全校学生成绩为A等大约有900人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.
如图,在直角坐标系xOy中,点A,B分别在x轴和y轴上,$\frac{OA}{OB}=\frac{3}{4}$,∠AOB的角平分线与OA的垂直平分线交于点C,与AB交于点D,反比例函数y=$\frac{k}{x}$的图象过点C,若以CD为边的正方形的面积等于 $\frac{2}{7}$,则k的值是7.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).
如图,在△ABC中,点D是边AC的中点,如果$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{BD}$=$\frac{1}{2}$$\overrightarrow{b}$-$\frac{1}{2}$$\overrightarrow{a}$(用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.
已知,一次函数y=x与二次函数y=x2+bx+c的图象相交于原点O 和点A(4,4)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com