
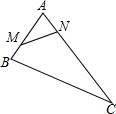
 如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似?
如图,在△ABC中,AB=8,AC=16,点M从点B开始沿BA边向点A以2个单位长度/秒的速度移动,点N从点A开始沿AC边向点C以4个单位长度/秒的速度移动.如果点M、N分别从点B、A同时出发,移动几秒,△AMN与△ABC相似? 分析 设移动x秒,△AMN与△ABC相似,则BM=2x,AN=4x,所以AM=AB-BM=8-2x,由于∠MAN=∠CAB,根据两组对应边的比相等且夹角对应相等的两个三角形相似进行分类讨论:当$\frac{AM}{AB}$=$\frac{AN}{AC}$时,△AMN∽△ABC,当$\frac{AM}{AC}$=$\frac{AN}{AB}$时,△AMN∽△ACB,然后分别利用相似比求x的值即可.
解答 解:设移动x秒,△AMN与△ABC相似,则BM=2x,AN=4x,
∴AM=AB-BM=8-2x,
∵∠MAN=∠CAB,
∴当$\frac{AM}{AB}$=$\frac{AN}{AC}$时,△AMN∽△ABC,即$\frac{8-2x}{8}$=$\frac{4x}{16}$,解得x=3,
当$\frac{AM}{AC}$=$\frac{AN}{AB}$时,△AMN∽△ACB,即$\frac{8-2x}{16}$=$\frac{4x}{8}$,解得x=$\frac{4}{5}$.
答:如果点M、N分别从点B、A同时出发,移动$\frac{4}{5}$秒或3秒时,△AMN与△ABC相似.
点评 本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的两个三角形相似.也考查了分类讨论的思想.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分.
如图,在?ABCD中,点E,F分别在边AD,BC上,且BF=DE,AF与DC的延长线交于点H,CE与BA的延长线交于点G,求证:AC与GH互相平分.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com