
 如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′
如图,在平面直角坐标系中,经过A(1,3),P(0,b)(b>0,b≠3)的直线交x轴于点B,经过P作PQ⊥AP,交x轴于点Q(m,0),作点P关于x轴的对称点为P′,连接AQ,QP′BP′分析 (1)过点A作AC⊥y轴于C,由题意得出:AC=1,CP=3-b,PO=b,OQ=m,证出∠APC=∠PQO,证明△ACP∽△POQ,得出比例式$\frac{OQ}{CP}=\frac{OP}{AC}$,得出OQ=3b-b2即可;
(2)证明四边形BPQP′是正方形,得出OQ=OP,①当0<b<3时,3b-b2=b,解得:b=2;②当b>3时,b2-3b=b,解得:b=4;
(3)分情况讨论:①当0<b<3时,由题意得出△APQ与以P、O、Q为顶点的三角形相似;当∠PQO=∠AQP时,由三角形相似得出比例式,得出b的值;
当∠PQO=∠PAQ时,证出AQ∥y轴,得出OQ=AC=1,即3b-b2=1,解方程即可;
②当b>3时;证出OQ=AC,得出方程:b2-3b=1,解方程即可.
解答 解:(1)过点A作AC⊥y轴于C,如图1所示: 根据题意得:AC=1,CP=3-b,PO=b,OQ=m,∠APQ=∠ACO=∠POQ=90°,
根据题意得:AC=1,CP=3-b,PO=b,OQ=m,∠APQ=∠ACO=∠POQ=90°,
∴∠APC+∠OPQ=90°,∠PQO+∠OPQ=90°,
∴∠APC=∠PQO,
∴△ACP∽△POQ,
∴$\frac{OQ}{CP}=\frac{OP}{AC}$,
即$\frac{OQ}{3-b}=\frac{b}{1}$,
∴OQ=3b-b2,
∴m=3b-b2;
(2)根据题意得:BP′=BP,PQ=P′Q,
∵BP′=PQ,
∴BP′=BP=PQ=P′Q,
∴四边形BPQP′是菱形,
∵∠APQ=90°,
∴∠BPQ=90°,
∴四边形BPQP′是正方形,
∴OQ=OP,
当0<b<3时,3b-b2=b,
解得:b=2;
当b>3时,b2-3b=b,
解得:b=4;
∴当BP′=PQ时,b的值为:2或4;
(3)存在;分情况讨论:
①当0<b<3时,
∵△ACP∽△POQ,△POQ≌△P′OQ,
∴△APQ与以P、O、Q为顶点的三角形相似;
当∠PQO=∠AQP时,
$\frac{OP}{AP}=\frac{OQ}{PQ}$,
即$\frac{b}{\sqrt{1+(3-b)^{2}}}=\frac{3b-{b}^{2}}{\sqrt{{b}^{2}+(3b-{b}^{2})^{2}}}$,
解得:b=$\frac{3}{2}$;
当∠PQO=∠PAQ时,∠APC=∠PQO,
∴∠APC=∠PAQ,
∴AQ∥y轴,
∴OQ=AC=1,
即3b-b2=1,
解得:b=$\frac{3±\sqrt{5}}{2}$;
②当b>3时,AQ与y轴交于D点,如图2所示: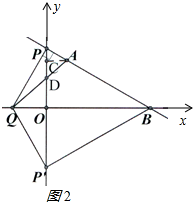 ∵∠OPQ=∠AQP,
∵∠OPQ=∠AQP,
∴PD=QD,
∵∠QPO+∠APO=∠PQA+∠PAQ,
∴∠APO=∠QAP,
∴PD=AD=QD,
∴$\frac{AC}{OQ}=\frac{AD}{QD}$=1,
∴OQ=AC,
∴b2-3b=1,
解得:b=$\frac{3±\sqrt{13}}{2}$,
∵b>0,
∴b=$\frac{3+\sqrt{13}}{2}$;
综上所述:当b=$\frac{3+\sqrt{13}}{2}$,或$\frac{3±\sqrt{5}}{2}$,或$\frac{3}{2}$时,△APQ∽△POQ.
点评 本题是相似形综合题目;考查了相似三角形的判定与性质、正方形的判定与性质、解方程等知识;本题难度较大,综合性强,特别是(2)(3)中,需要通过作辅助线进行分类讨论和证明三角形相似才能得出结果.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}+1}{{x}^{2}-1}$ | B. | $\frac{x+1}{{x}^{2}}$ | C. | $\frac{x-1}{{x}^{2}+1}$ | D. | $\frac{{x}^{2}}{x+1}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )| A. |  | B. | 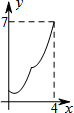 | C. | 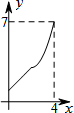 | D. | 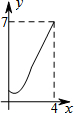 ? ? |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
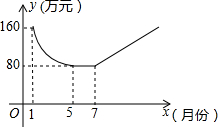 保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.
保护生态环境,建设绿色社会已经从理念变为人们的行动,某化工厂2011年1月的利润为160万元,设2011年1月为第1个月,第x个月的利润为y万元,由于排污超标,该厂决定从2011年1月底起适当限产,并投入资金进行治污改造,整个工程经过治污改造、调试、全面投产是三个时期,经测算:从1月到5月为治污改造期,y是x的二次函数,且其图象的顶点为(5,80),到5月底治污改造工程顺利完成,进接的6月、7月为调试期,月利润和5月份持平,调试期过后,设备全面投产,该厂每月利润比前一个月增加15万元,如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
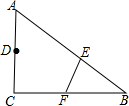 如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.
如图,在△ABC中,∠C=90°,AC=6,BC=9,将△ABC沿EF翻折点B恰好落在CA的中点D处,则折痕EF的长为$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.
如图所示,在△ABC中,∠ACB=90°,△BEF与△CEF成轴对称,△CEF沿CE翻折与△CED重合,且△ACD≌△EBF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有旗杆BC,旗杆顶端B点与A点有一条彩带相连.若AB=10米,则旗杆BC的高度为( )| A. | 5米 | B. | 6米 | C. | 8米 | D. | (3+$\sqrt{5}$)米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com