练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在四边形ABCD中，如果AD//BC，AE//CF，BE=DF，那么下列等式中错误的是（ ）

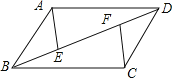
    A. ∠DAE=∠BCFB. AB=CDC. ∠BAE=∠DCFD. ∠ABE=∠EBC

    【答案】D

    【解析】

    利用AD//BC，AE//CF证得角等，证出△AED≌CFB，即可判断A选项；利用全等三角形的性质得到AE=CF，进而证出△ABE≌△CDF，即可判断B、C选项，即可完成.

    ∵AD//BC，AE//CF

    ∴∠AED=∠CFB , ∠DBC=∠ADB

    ∵BE=DF

    ∴BE+EF=DF+EF

    即BF=ED

    ∴△AED≌CFB（ASA）

    ∴∠DAE=∠BCF

    故A选项正确；

    ∵△AED≌CFB

    ∴AE=CF

    ∵∠AEB+∠AED=180°，∠CFB+∠DFC=180°，∠AED=∠CFB

    ∴∠AEB=∠DFC

    又∵BE=FD

    ∴△ABE≌△CDF（SAS）

    ∴AB=CD，∠BAE=∠DCF

    故B、C选项正确；

    故选D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知：如图，点E，F分别在AB，CD上，AF⊥CE，垂足为点O，∠1＝∠B，

    ∠A+∠2＝90°．求证：AB∥CD．

    证明：如图，

    ∵∠1＝∠B（已知）

    ∴CE∥BF（同位角相等，两直线平行）

    ______________

    ∴∠AFC+∠2＝90°（等式性质）

    ∵∠A+∠2＝90°（已知）

    ∴∠AFC＝∠A（同角或等角的余角相等）

    ∴AB∥CD（内错角相等，两直线平行）

    请你仔细观察下列序号所代表的内容：

    ①∴∠AOE＝90°（垂直的定义）

    ②∴∠AFB＝90°（等量代换）

    ③∵AF⊥CE（已知）

    ④∵∠AFC+∠AFB+∠2＝180°（平角的定义）

    ⑤∴∠AOE＝∠AFB（两直线平行，同位角相等）

    横线处应填写的过程，顺序正确的是（　　）

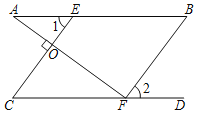
    A.⑤③①②④B.③④①②⑤C.⑤④③①②D.⑤②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程x2＋(2m＋1)x＋m2－4＝0.

    (1)当m为何值时，方程有两个不相等的实数根？

    (2)若边长为5的菱形的两条对角线的长分别为方程两根的2倍，求m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平行四边形中，，，是上的一个动点，由向运动（与、不重合），速度为每秒，是延长线上一点，与点以相同的速度由向延长线方向运动（不与重合），连结交AB于．

    （1）如图1，若，，求点P运动几秒后，.

    （2）在（1）的条件下，作于F，在运动过程中，线段长度是否发生变化，如果不变，求出的长；如果变化，请说明理由.

    （3）如图3，当时，平行四边形的面积是，那么在运动中是否存在某一时刻，点P，Q关于点E成中心对称，若存在，求出a的值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为m，宽为n)的盒子底部(如图②)，盒子底面未被卡片覆盖的部分用阴影表示，则图②中两块阴影部分的周长和是（ ）

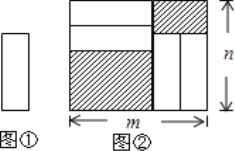
    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，3×3的方格分为上中下三层，第一层有一枚黑色方块甲，可在方格A、B、C中移动，第二层有两枚固定不动的黑色方块，第三层有一枚黑色方块乙，可在方格D、E、F中移动，甲、乙移入方格后，四枚黑色方块构成各种拼图．

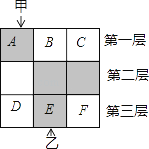
    （1）若乙固定在E处，移动甲后黑色方块构成的拼图是轴对称图形的概率是________．

    （2）若甲、乙均可在本层移动．

    ①用树形图或列表法求出黑色方块所构拼图是轴对称图形的概率．

    ②黑色方块所构拼图是中心对称图形的概率.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】公元初，中美洲玛雅人使用的一种数字系统与其他计数方式都不相同，它采用二十进位制但只有3个符号，用点“●”、划“__________”、卵形“”来表示我们所使用的自然数，如自然数1～19的表示见下表，另外在任何数的下方加一个卵形，就表示把这个数扩大到它的20倍，如表中20和100的表示.

    （1）玛雅符号表示的自然数是__________；

    （2）请你在右边的方框中画出表示自然数280的玛雅符号：

    自然数

    1

    2

    3

    4

    5

    玛雅符号

    ●

    ●●

    ●●●

    ●●●●

    _______

    自然数

    6

    7

    8

    9

    10

    玛雅符号

    自然数

    11

    12

    …

    15

    16

    玛雅符号

    …

    自然数

    …

    19

    20

    …

    100

    玛雅符号

    …

    …

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：公路旁有两个高度相等的路灯AB、CD.数学老师杨柳上午上学时发现路灯B在太阳光下的影子恰好落到里程碑E处，他自己的影子恰好落在路灯CD的底部C处．晚自习放学时，站在上午同一个地方，发现在路灯CD的灯光下自己的影子恰好落在里程碑E处．

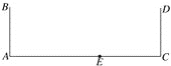
    (1)在图中画出杨老师的位置(用线段FG表示)，并画出光线，标明(太阳光、灯光)；

    (2)若上午上学时候高1米的木棒的影子为2米，杨老师身高为1.5米，他离里程碑E恰5米，求路灯高．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某一公路的道路维修工程，准备从甲、乙两个工程队选一个队单独完成．根据两队每天的工程费用和每天完成的工程量可知，若由两队合做此项维修工程，6天可以完成，共需工程费用385200元，若单独完成此项维修工程，甲队比乙队少用5天，每天的工程费用甲队比乙队多4000元，（1）若甲单独完成需要多少天？（2）从节省资金的角度考虑，应该选择哪个工程队？

    查看答案和解析>>

    同步练习册答案