
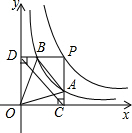
 两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号)
两个反比例函数y=$\frac{k}{x}$(k>1)和y=$\frac{1}{x}$在第一象限内的图象如图所示,点P在y=$\frac{k}{x}$的图象上,PC⊥x轴于点C,交y=$\frac{1}{x}$的图象于点A,PD⊥y轴于点D,交y=$\frac{1}{x}$的图象于点B,BE⊥x轴于点E,当点P在y=$\frac{k}{x}$图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是①③④(填序号) 分析 设出点P的坐标,由此可得出A、C、B、D点的坐标,由点的坐标即可表示出各线段的长度,根据线段间的比例关系即可得出BA∥DC,即①成立;找出当PA=PB时,m的值,由此发现②不一定成立;③根据反比例函数系数k的几何意义可得出三角形OBD、OAC以及矩形OCPD的面积,分割图形即可得出S四边形PAOB=k-1,即③成立;根据各边长度计算出S梯形BECA,结合三角形的面积公式求出S△OBA,发现二者相等,由此得知④成立.综上即可得出结论.
解答 解:设点P的坐标为(m,$\frac{k}{m}$),则点A(m,$\frac{1}{m}$),点C(m,0),点B($\frac{m}{k}$,$\frac{k}{m}$),点D(0,$\frac{k}{m}$),
∴PB=m-$\frac{m}{k}$=$\frac{k-1}{k}m$,PD=m,PA=$\frac{k}{m}$-$\frac{1}{m}$=$\frac{k-1}{m}$,PD=m,PC=$\frac{k}{m}$,
∵$\frac{PB}{PD}$=$\frac{k-1}{k}$,$\frac{PA}{PC}$=$\frac{k-1}{k}$=$\frac{PB}{PD}$,
∴BA∥DC,①成立;
∵PB=$\frac{k-1}{k}m$,PA=$\frac{k-1}{m}$,
∴当m2=k时,PA=PB,②不成立;
S矩形OCPD=k,S△OBD=$\frac{1}{2}$,S△OAC=$\frac{1}{2}$,
S四边形PAOB=S矩形OCPD-S△OBD-S△OBD=k-1,
∵k为固定值,
∴③成立;
S梯形BECA=$\frac{1}{2}$(AC+BE)•EC=$\frac{1}{2}$($\frac{1}{m}$+$\frac{k}{m}$)•(m-$\frac{m}{k}$)=$\frac{{k}^{2}-1}{2k}$,S△OBA=S四边形PAOB-S△PAB=k-1-$\frac{1}{2}$(m-$\frac{m}{k}$)•($\frac{k}{m}$-$\frac{1}{m}$)=$\frac{{k}^{2}-1}{2k}$,
∴S梯形BECA=S△OBA,④成立.
综上可知:一定正确的为①③④.
故答案为:①③④.
点评 本题考查了反比例函数系数k的几何意义、反比例函数的性质以及三角形的面积公式,解题的关键是设出点P坐标,表示出其他各点的坐标.本题属于中档题,难度不大,但运算过程较繁琐,解决该题型题目时,结合点的坐标以及反比例函数系数k的几何意义,表示出来图形各部分的面积是关键.


科目:初中数学 来源: 题型:选择题
| A. | 了解某班同学的体重情况 | B. | 了解我省初中学生的兴趣爱好情况 | ||
| C. | 了解一批电灯泡的使用寿命 | D. | 了解我省农民工的年收入情况 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
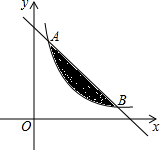 平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点.如图,直线y=-x+7和反比例函数y=$\frac{6}{x}$(x>0)的图象交于A,B两点,则落在图中阴影部分(不包含边界)内的整点个数有( )个.
平面直角坐标系中,我们把横坐标、纵坐标都是整数的点称为整点.如图,直线y=-x+7和反比例函数y=$\frac{6}{x}$(x>0)的图象交于A,B两点,则落在图中阴影部分(不包含边界)内的整点个数有( )个.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
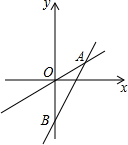 正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),且OB=10.
正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),且OB=10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com