
分析 如图所示,当x=1,y≤0抛物线与线段PQ有交点,列出不等式即可解决问题.
解答 解:①∵二次函数y=x2+2ax+3的图象与线段PQ有交点,抛物线与y轴交于(0,3),开口向上,可知如图所示,满足条件,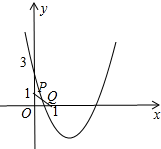
当x=1,y≤0抛物线与线段PQ有交点,
∴1+2a+3≤0,
∴a≤-2,
②如图,如果是这种情形,由题意$\left\{\begin{array}{l}{y=-x+1}\\{y={x}^{2}+2ax+3}\end{array}\right.$,消去y得到x2+(2a+1)x+2=0,
因为有交点,设交点的横坐标为x1,x2,
∵x1•x2=2,与0<x1<1,0<x2<1矛盾,
∴这种情形不存在.
综上所述,a≤-2.
故答案为a≤-2.
点评 本题考查二次函数图象上的点的坐标特征,解题的关键是学会利用图象解决问题,把问题转化为不等式,属于中考常考题型.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:选择题
 如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=90°,若OA=4,则图中圆环的面积大小为( )
如图,以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C,若∠AOB=90°,若OA=4,则图中圆环的面积大小为( )| A. | 2π | B. | 4π | C. | 6π | D. | 8π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{12}{5}$ | C. | $\frac{12}{13}$ | D. | $\frac{5}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,AD是△ABC的外角∠CAE的平分线,∠B=40°,∠DAE=55°,则∠ACB的度数是( )
如图,AD是△ABC的外角∠CAE的平分线,∠B=40°,∠DAE=55°,则∠ACB的度数是( )| A. | 70° | B. | 80° | C. | 100° | D. | 110° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ∠A=90° | B. | ∠B=90° | C. | ∠C=90° | D. | ∠A=60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,数轴上表示1和$\sqrt{3}$的对应点分别为A,B,点B到点A的距离与点C到点O的距离相等,设点C表示的数为x,请你写出数x的值.
如图,数轴上表示1和$\sqrt{3}$的对应点分别为A,B,点B到点A的距离与点C到点O的距离相等,设点C表示的数为x,请你写出数x的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com