
【题目】如图1,在平面直角坐标系中,△AOB为等腰直角三角形,A(4,4).
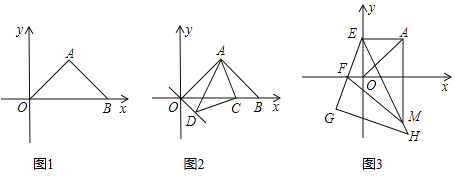
(1)点B坐标为
(2)如图2,若C为x轴正半轴上一动点,以AC为直角边作等腰Rt△ACD,∠ACD=90,连OD,求∠AOD的度数;
(3)如图3,过点A作y轴的垂线交y轴于点E,F为x轴负半轴上一点,点G在EF的延长线上,以EG为直角边作等腰Rt△EGH,过点A作x轴垂线交EH于点M,连FM,等式![]() =1是否成立?若成立,请证明;若不成立,说明理由.
=1是否成立?若成立,请证明;若不成立,说明理由.
【答案】(1)(8,0);(2)90°;(3)![]() =1成立,理由详见解析.
=1成立,理由详见解析.
【解析】
(1)因为△AOB为等腰直角三角形,A(4,4),作AE⊥OB于E,则B点坐标可求;(2)作AE⊥OB于E,DF⊥OB于F,求证△DFC≌△CEA,再根据等量变换,证明△AOB为等腰直角三角形,则∠AOD的度数可求;(3)等式成立.在AM上截取AN=OF,连EN,易证△EAN≌△EOF,再根据角与角之间的关系,证明△NEM≌△FEM,则有AM-MF=OF,即可求证等式成立.
(1)作AE⊥OB于E,

∵A(4,4),
∴OE=4,
∵△AOB为等腰直角三角形,且AE⊥OB,
∴OE=EB=4,
∴OB=8,
∴B(8,0);
故答案为:(8,0);
(2)作AE⊥OB于E,DF⊥OB于F,
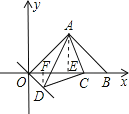
∵△ACD为等腰直角三角形,
∴AC=DC,∠ACD=90°
即∠ACF+∠DCF=90°,
∵∠FDC+∠DCF=90°,
∴∠ACF=∠FDC,
又∵∠DFC=∠AEC=90°,
∴△DFC≌△CEA,
∴EC=DF,FC=AE,
∵A(4,4),
∴AE=OE=4,
∴FC=OE,
即OF+EF=CE+EF,
∴OF=CE,
∴OF=DF,
∴∠DOF=45°
∵△AOB为等腰直角三角形,
∴∠AOB=45°,
∴∠AOD=∠AOB+∠DOF=90°;
(3)成立,理由如下:
在AM上截取AN=OF,连EN.

∵A(4,4),
∴AE=OE=4,
又∵∠EAN=∠EOF=90°,AN=OF,
∴△EAN≌△EOF(SAS)
∴∠OEF=∠AEN,EF=EN,
又∵△EGH为等腰直角三角形,
∴∠GEH=45°,
即∠OEF+∠OEM=45°,
∴∠AEN+∠OEM=45°
又∵∠AEO=90°,
∴∠NEM=45°=∠FEM,
又∵EM=EM,
∴△NEM≌△FEM(SAS),
∴MN=MF,
∴AM-MF=AM-MN=AN,
∴AM-MF=OF,
即![]() =1.
=1.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数![]() 的图象上,点C,D在反比例函数
的图象上,点C,D在反比例函数![]() 的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
的图象上,AC//BD//y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为( )
,则k的值为( )

A. 4 B. 3 C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD、CE是△ABC的高,AF=BC,BE=3,AE=5.
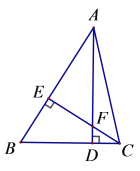
(1)图中有全等的三角形吗?请找出来并加以证明;
(2)求线段CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC, ∠ABC=90 ,点E在BD上,点F在射线CD上,AE=EF,∠AEF=90 .
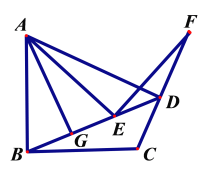
(1)若∠ABE=∠AEB,AG⊥BD,垂足为G,求证:BG=GE.
(2)在(1)的条件下,猜想线段CD与DF的数量关系,并证明你的猜想.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】威远人民商场准备购进甲、乙两种牛奶进行销售,若甲种牛奶的进价比乙种牛奶的进价每件少5元,其用90元购进甲种牛奶的数量与用100元购进乙种牛奶的数量相同.
(1)求甲种牛奶、乙种牛奶的进价分别是多少元?
(2)若该商场购进甲种牛奶的数量是乙种牛奶的3倍少5件,两种牛奶的总数不超过95件,该商场甲种牛奶的销售价格为49元,乙种牛奶的销售价格为每件55元,则购进的甲、乙两种牛奶全部售出后,可使销售的总利润(利润=售价﹣进价)超过371元,请通过计算求出该商场购进甲、乙两种牛奶有哪几种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的个数是( )
(1)a和0都是单项式
(2)多项式![]() 的次数是3
的次数是3
(3)单项式![]() 的系数是
的系数是![]()
(4)x2+2xy-y2可读作x2、2xy、-y2的和
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
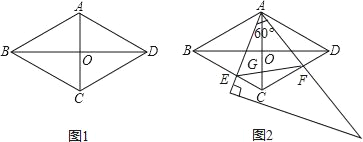
【题目】如图1,在菱形ABCD中,AC=2,BD=2![]() ,AC、BD相交于点O.
,AC、BD相交于点O.
(1)AB的长为 ;
(2)如图2,将一个足够大的直角三角板60°角的顶点放在菱形ABCD的顶点A处,绕点A左右旋转,其中三角板60°角的两边分别与边BC,CD相交于点E,F,连接EF与AC相交于点G.
①求证:△ABE≌△ACF;
②判断△AEF是哪一种特殊三角形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com