
 如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.
如图,在矩形纸片ABCD中,AD=5,AB=3,点E为BC上一点,沿着AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D.分析 (1)根据平移的性质得到AE∥DE′,AE=DE′,则由此判定四边形AEE′D是平行四边形;然后根据菱形的性质求得AE=AD=5,根据勾股定理即可求得BE;
(2)根据勾股定理,可得答案.
解答 解:(1)当BE=4时,四边形AEE'D是菱形.
理由:由△ABE平移至△DCE'的位置,可知
AD∥EE'且AD=EE'.
∴四边形AEE'D是平行四边形.
∵四边形AEE'D是菱形,
∴AE=AD=5,
∵AB=3,∠B=90°,
∴BE=$\sqrt{A{E}^{2}-A{B}^{2}}$=4.
∴当BE=4时,四边形AEE'D是菱形.
(2)∵BC=AD=5,DC=AB=3,BE=4,
∴CE=1,BE'=9.
在Rt△DCE中,$DE=\sqrt{{3^2}+{1^2}}=\sqrt{10}$.
在Rt△ABE'中,$AE'=\sqrt{{3^2}+{9^2}}=3\sqrt{10}$.
点评 本题考查了菱形的性质、图形的剪拼以及平移的性质.通过解答该题,使学生学会能够灵活运用菱形、勾股定理知识解决有关问题.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:选择题
| A. | 某个对象出现的次数称为频率 | |
| B. | 要了解某品牌运动鞋使用寿命可用普查 | |
| C. | 没有水分种子发芽是随机事件 | |
| D. | 折线统计图用于表示数据变化的特征和趋势 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
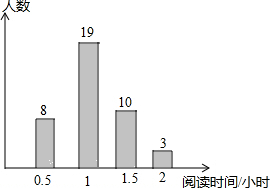 某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )
某中学组织了一次读书活动,随机调查了部分学生平均每天的阅读时间,统计结果如图所示,则在本次调查中,阅读时间的中位数和众数分别是( )| A. | 2,1 | B. | 1,1.5 | C. | 1,2 | D. | 1,1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每人加工零件数 | 54 | 45 | 30 | 24 | 21 | 12 |
| 人 数 | 1 | 1 | 2 | 6 | 3 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{9}{4}$ | D. | -$\frac{9}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com