
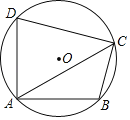
【题目】已知四边形ABCD内接于⊙O,∠DAB=90°.
(Ⅰ)若AB=AD,求∠ACB的度数;
(Ⅱ)连接AC,若AD=8,AB=6,对角线AC平分∠DAB,求AC的长.
【答案】(Ⅰ)45°;(Ⅱ)7![]() .
.
【解析】
(Ⅰ)连接BD,根据圆周角定理得到BD为直径,推出△ABD为等腰直角三角形,于是得到∠ACB=∠ADB=45°;
(Ⅱ)如图2,作BH⊥AC于H,根据勾股定理得到BD=10,根据角平分线的定义得到∠BAC=∠BAC=45°,推出△CDB为等腰直角三角形,得到BC=![]() BD=
BD=![]() ,解直角三角形即可得到结论.
,解直角三角形即可得到结论.
(Ⅰ)连接BD,

∵∠DAB=90°,
∴BD为直径,
∵AD=AB,
∴△ABD为等腰直角三角形,
∴∠ACB=∠ADB=45°;
(Ⅱ)如图,作BH⊥AC于H,
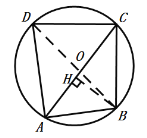
∵∠DAB=90°,
∴BD为直径,![]() ,
,
∴∠BCD=90°,
∵AC平分∠DAB,
∴∠BAC=∠BAC=45°,
∴∠CBD=∠BDC=45°,
∴△CDB为等腰直角三角形,
∴![]() ,
,
在Rt△ABH中,AH=BH=![]() AB=3
AB=3![]() ,
,
在Rt△BCH中,![]() ,
,
∴![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
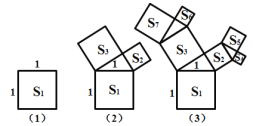
【题目】请你仔细观察下面一组图形,依据其变化规律推断第(5)个图形中所有正方形面积之和为____________(其中图 中出现的三角形均是直角三角形,四边形均是正方形).
查看答案和解析>>
科目:初中数学 来源: 题型:
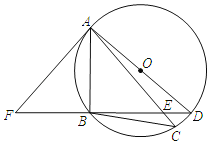
【题目】如图,AD是⊙O的直径,弧BA=弧BC,BD交AC于点E,点F在DB的延长线上,且∠BAF=∠C.
(1)求证:AF是⊙O的切线;
(2)求证:△ABE∽△DBA;
(3)若BD=8,BE=6,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“手拉手”数学学习互助小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究时,遇到以下问题,请你逐一加以解答:
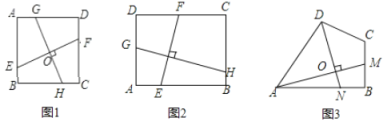
(1)如图1,正方形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,则EF GH;(填“>”“=”或“<”)
(2)如图2,矩形ABCD中,EF⊥GH,EF分别交AB,CD于点E,F,GH分别交AD,BC于点G,H,求证:![]() =
=![]() ;
;
(3)如图3,四边形ABCD中,∠ABC=∠ADC=90°,BC=3,CD=5,AD=7.5,AM⊥DN,点M,N分别在边BC,AB上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() .已知A(-2,0)、B(6,0)、D(0,3)反比例函数
.已知A(-2,0)、B(6,0)、D(0,3)反比例函数![]() 的图象经过点
的图象经过点![]() .
.
(1)求点![]() 的坐标和反比例函数
的坐标和反比例函数![]() 的解析式;
的解析式;
(2)将四边形![]() 沿
沿![]() 轴向上平移
轴向上平移![]() 个单位长度得到四边形
个单位长度得到四边形![]() ,问点
,问点![]() 是否落在(1)中的反比例函数的图象上?
是否落在(1)中的反比例函数的图象上?

查看答案和解析>>
科目:初中数学 来源: 题型:
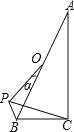
【题目】如图,△ABC中,∠ACB=90°,∠BAC=20°,点O是AB的中点,将OB绕点O顺时针旋转α角时(0°<α<180°),得到OP,当△ACP为等腰三角形时,α的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的的直径,弦CD与AB相交,∠BCD=25°。
(1)如图1,求∠ABD的大小;
(2)如图2,过点D作O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的度数。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com