
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
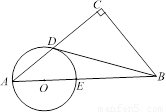
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
(1)见解析;(2)BD=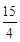 .
.
【解析】
试题分析:(1)要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可;
(2)通过作辅助线,根据已知条件求出∠CBD的度数,在Rt△BCD中求解即可.
试题解析:
(1)直线BD与⊙O的位置关系是相切.
证明:连结OD,DE.
∵∠C=90°,
∴∠CBD+∠CDB=90°.
∵∠A=∠CBD,
∴∠A+∠CDB=90°.
∵OD=OA,
∴∠A=∠ADO.
∴∠ADO+∠CDB=90°.
∴∠ODB=180°-90°=90°.
∴OD⊥BD.
∵OD为半径,
∴BD是⊙O切线.
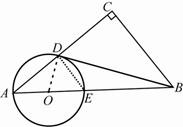
(2)∵AD:AO=8:5,
∴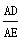 =
=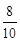 .
.
∴由勾股定理得AD:DE:AE=8:6:10.
∵∠C=90°,∠CBD=∠A.
∴△BCD∽△ADE.
∴DC:BC:BD=DE:AD:AE=6:8:10.
∵BC=3,
∴BD=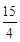 .
.
考点:1.圆切线的判定;2.相似三角形的性质.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
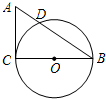 在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.
在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
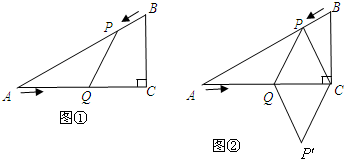
 (2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
(2013•丹东一模)在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com