
【题目】如图,在四边形ABCD中,对角线AC⊥BD,垂足为O,点E,F,G,H分别为边AB,BC,CD,AD的中点.若AC=10,BD=6,则四边形EFGH的面积为( )

A. 15B. 20C. 30D. 60
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某中学随机抽取部分学生进行科技知识的调查测试,测试成绩分为A,B,C,D,E五个等级,通过对测试成绩的分析,得到如下条形统计图:
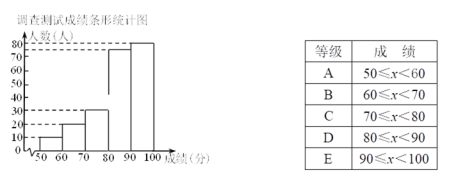
请根据所给信息,解答下列问题:
(1)试分析本次调查测试成绩的“中位数”在哪个等级;
(2)若本次调查测试成绩在80分及以上为优秀,该中学共有800人,请估计全校测试成绩为优秀的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨实验学校为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买1副围棋和1副中国象棋需用26元;若购买8副围棋和3副中国象棋需用158元;
(1)求每副围棋和每副中国象棋各多少元;
(2)实验中学决定购买围棋和中国象棋共40副,总费用550元,那么实验中学可以购买多少副围棋.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据要求,解答下列问题:
(1)①方程x2﹣x﹣2=0的解为 ;
②方程x2﹣2x﹣3=0的解为 ;
③方程x2﹣3x﹣4=0的解为 ;
…
(2)根据以上方程特征及其解的特征,请猜想:
①方程x2﹣9x﹣10=0的解为 ;
②请用配方法解方程x2﹣9x﹣10=0,以验证猜想结论的正确性.
(3)应用:关于x的方程 的解为x1=﹣1,x2=n+1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在△ABC中,∠A=90°,AB=AC=1,P是AC上不与A、C重合的一动点,PQ⊥BC于Q,QR⊥AB于R.
(1)求证:PQ=CQ;
(2)设CP的长为x,QR的长为y,求y与x之间的函数关系式及自变量x的取值范围,并在平面直角坐标系作出函数图象.
(3)PR能否平行于BC?如果能,试求出x的值;若不能,请简述理由.
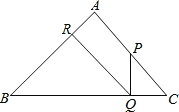
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y1=kx+4与y2=x+b的图象交于点A.则下列结论中错误的是( )
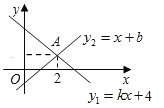
A. K<0,b>0B. 2k+4=2+b
C. y1=kx+4的图象与y轴交于点(0,4)D. 当x<2时,y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一条数轴上从左到右依次取A,B,C三个点,且使得点A,B到原点O的距离均为1个单位长度,点C到点A的距离为7个单位长度.
(1)在数轴上点A所表示的数是__________,点C所表示的数是_____________.
(2)若点P、Q分别从点A、C处出发,沿数轴以每秒1个单位长度和每秒3个单位长度的速度同时向左运动,运动时间为t秒,当P、Q两点相距为4个单位长度时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察思考:如图,线段AB上有两个点C、D,请分别写出以点A、B、C、D为端点的线段,并计算图中共有多少条线段;
(2)模型构建:如果线段上有m个点(包括线段的两个端点),则该线段上共有多少条线段?请说明你结论的正确性;
(3)拓展应用:某班45名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握多少次手?
请将这个问题转化为上述模型,并直接应用上述模型的结论解决问题.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线y=﹣![]() x+1交y轴于点B,交x轴于点A,抛物线y=﹣
x+1交y轴于点B,交x轴于点A,抛物线y=﹣![]() x2+bx+c经过点B,与直线y=﹣
x2+bx+c经过点B,与直线y=﹣![]() x+1交于点C(4,﹣2).
x+1交于点C(4,﹣2).
(1)求抛物线的解析式;
(2)如图,横坐标为m的点M在直线BC上方的抛物线上,过点M作ME∥y轴交直线BC于点E,以ME为直径的圆交直线BC于另一点D,当点E在x轴上时,求△DEM的周长.
(3)将△AOB绕坐标平面内的某一点按顺时针方向旋转90°,得到△A1O1B1,点A,O,B的对应点分别是点A1,O1,B1,若△A1O1B1的两个顶点恰好落在抛物线上,请直接写出点A1的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com