
分析 (1)把C(0,4),B(4,0)的坐标代入y=-$\frac{1}{4}$x2+bx+c,把问题转化为解方程组即可
(2)首先证明△ABC是等腰直角三角形,再证明△ACD≌△BCF,利用三角形的全等,得出∠ABF=∠ABC+∠CBF=90°,即可得出答案;
(3)先证明△ODC≌△DME(AAS),推出DM=OC=4,OD=EM,由OD=OB-BD=4-BD=DM-BD=BM,推出BM=EM,由∠EMB=90°,推出∠MBE=∠MEB=45°,由此即可解决问题.
(4)由(3)知,点E在射线BE上,当点D与点B重合时,BE=BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
解答 解:(1)把C(0,4),B(4,0)的坐标代入y=-$\frac{1}{4}$x2+bx+c得$\left\{\begin{array}{l}{c=4}\\{-4+4b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=0}\\{c=4}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{1}{4}$x2+4;
(2)证明:由(1)得到抛物线的解析式为y=-$\frac{1}{4}$x2+4;
令y=0,得x1=4,x2=-4,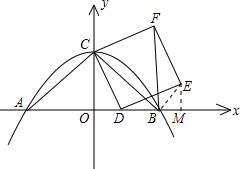
∴A(-4,0),B(4,0),
∴OA=OB=OC,
∴△ABC是等腰直角三角形;
如图,又∵四边形CDEF是正方形,
∴AC=BC,CD=CF,∠ACD=∠BCF,
在△ACD和△BCF中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCF}\\{CD=CF}\end{array}\right.$,
∴△ACD≌△BCF(SAS),
∴∠CBF=∠CAD=45°,
∴∠ABF=∠ABC+∠CBF=90°,
∴BF⊥AB;
(3)如图,连接BE,过点E作EM⊥x轴于点M.
∵∠ODC+∠EDM=90°,∠EDM+∠DEM=90°,
∴∠CDO=∠DEM,
在△ODC和△MED中,
$\left\{\begin{array}{l}{∠COD=∠EMD}\\{∠ODC=∠MED}\\{CD=DE}\end{array}\right.$,
∴△ODC≌△DME(AAS),
∴DM=OC=4,OD=EM,
∵OD=OB-BD=4-BD=DM-BD=BM,
∴BM=EM.
∵∠EMB=90°,
∴∠MBE=∠MEB=45°;
由(2)知,BF⊥AB,
∴∠FBE=∠FBM-∠MBE=45°;
(4)由(3)知,点E在射线BE上,当点D与点B重合时,BE=BC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$.
∴当D点沿x轴正方向移动到点B时,点E所走过的路线长是4$\sqrt{2}$,
故答案为4$\sqrt{2}$.
点评 本题考查二次函数综合题、待定系数法、全等三角形的判定与性质、正方形和等腰直角三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,(4)中弄清点E的轨迹是线段是关键,属于中考压轴题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
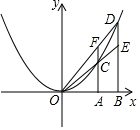 如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF
如图,在x轴上有两点A(m,0),B(n,0)(n>m>0),分别过点A,点B作x轴的垂线,交抛物线y=x2于点C,点D.直线OC交直线BD于点E,直线OD交直线AC于点F,点E,点F的纵坐标分别记作yE,yF查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
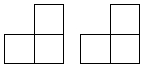 由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )
由一些大小相同的小正方形组成,下面的两个图分别是从正面和从上面看这个几何体得到的平面图形,那么组成该几何体所需的小正方形的个数为( )| A. | 4个 | B. | 4个或5个 | C. | 5个或6个 | D. | 6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )
在扇形OACB中,∠AOB=120°,⊙O′为弓形ACB的最大的内切圆,若AB的长为2π,则⊙O′的周长为( )| A. | π | B. | $\frac{2}{3}$π | C. | $\frac{3}{2}$π | D. | 2π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com