
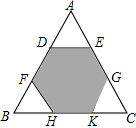
 如图,把边长为6的正三角形剪去三个三角形得到一个正六边形DFHKGE,求这个正六边形的面积.
如图,把边长为6的正三角形剪去三个三角形得到一个正六边形DFHKGE,求这个正六边形的面积.科目:初中数学 来源: 题型:
| 列举 | 猜想 |
| 3,4,5 | 32=4+5 |
| 5,12,13 | 52=12+13 |
| 7,24,25 | 72=24+25 |
| … | … |
| 13,b,c | 132=b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:
| AB |
| A′B′ |
| BC |
| B′C′ |
| BC |
| B′C′ |
| AC |
| A′C′ |
| A、1 | B、2 | C、3 | D、4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
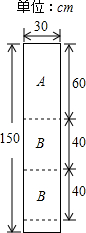 某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)| 裁法一 | 裁法二 | 裁法三 | |
| A型板材块数 | 1 | 2 | 0 |
| B型板材块数 | 2 | m | n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )
如图,P为∠AOB内一定点,M、N分别是射线OA、OB上一点,当△PMN周长最小时,∠OPM=50°,则∠AOB=( )| A、40° | B、45° |
| C、50° | D、55° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com