
分析 当k=0时,为一次函数,则与x轴和y轴各有一个交点满足条件;当k≠0时,当二次函数不过原点时,可知函数与x轴只有一个交点,则根据对应一元二次方程的判别式为可求得k的值;当二次函数过原点时也满足条件,可求得k的值.
解答 解:
当k=0时,函数y=-2x-2,与x轴和y轴各有一个交点,满足条件;
当k≠0时,若二次函数不过原点,令y=0可得kx2-2x-k-2=0,由函数与y轴交于点(0,-k-2),则与x轴只能有一个交点,
∴△=(-2)2-4k(-k-2)=0,解得k=-1;
若二次函数过原点,也满足条件,此时-k-2=0,解得k=-2;
综上可知k的值为0或-1或-2,
故答案为:0或-1或-2.
点评 本题主要考查二次函数与坐标轴的交点,掌握二次函数的交点个数与对应一元二次方程根的个数的关系是解题的关键,注意分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | a<b | B. | a>b | C. | a≥b | D. | a=b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
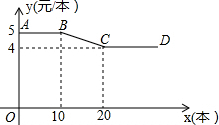 开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.
开学初,小明到文具批发部一次性购买某种笔记本,该文具批发部规定:这种笔记本售价y(元/本)与购买数量x(本)之间的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
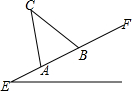 如图,为迎接全国文明城市检查,某单位准备在一斜坡EF上安装衣服悬挂“社会主义核心价值观”宣传牌的金属架A-C-B,若CA与地面垂直,斜坡的坡角∠E=30°,∠C=45°,小王测得从A到B的距离是5m,已知每米金属架106元,请你帮该单位算一下安装这副金属架共需多少元(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449,结果保留整数).
如图,为迎接全国文明城市检查,某单位准备在一斜坡EF上安装衣服悬挂“社会主义核心价值观”宣传牌的金属架A-C-B,若CA与地面垂直,斜坡的坡角∠E=30°,∠C=45°,小王测得从A到B的距离是5m,已知每米金属架106元,请你帮该单位算一下安装这副金属架共需多少元(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,$\sqrt{5}$≈2.236,$\sqrt{6}$≈2.449,结果保留整数).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 当a>0时,x1<m<n<x2 | |
| B. | 当a<0时,m<x1<x2<n | |
| C. | 存在m+n=x1+x2 | |
| D. | y=ax2+bx+c-2015与x轴的交点坐标不可能是(x1,0),(x2,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com