
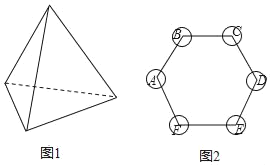
����Ŀ��ͼ����һö�ʵؾ��ȵ�����������״�����ӣ�ÿ�����Ϸֱ��������2��3��4��5��ͼ����һ�������������̣���ͨ�������ӵķ�ʽ��������Ϸ�������ǣ�����ö�����������������������������ϣ������棩�������Ǽ����ʹ�ͼ�е�A�㿪ʼ����˳ʱ�뷽�����������������㣬�ڶ��δӵ�һ�ε��յ㴦��ʼ������һ�εķ�����������
��1�������һ�����ӣ���������������C���ĸ������� ����
��2��������������ӣ��û���״ͼ���б��ķ�����������������������C���ĸ��ʣ�
���𰸡���1��![]() ����2��
����2��![]() ��
��
��������
��1������������Ϊ2ʱ�����Ե����C���ݴ˽�һ����⼴�ɣ�
��2�����������ӵ����ֺ�һ������2С��10����ֻ��Ҫ��һ�ܺ��C���ɣ���ʱ��Ҫ8�����ݴ˽�һ���б��ó����п����ԣ�Ȼ���ٴμ��Լ��㼴��.
��1�������һ�����ӣ���������������C����Ҫ������������������C�ĸ����൱������2���ֵĸ��ʣ�������2���ֵĸ�����![]() ��
��
�ʴ�Ϊ![]() ��
��
��2���б���ͼ��
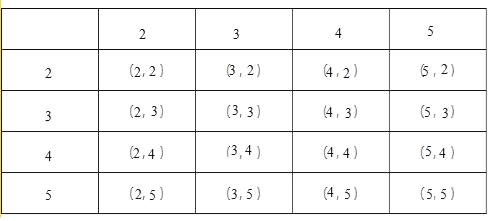
����16�ֿ��ܣ���Ϊ8���Ե����C����3�����Σ���������������������C���ĸ���Ϊ![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
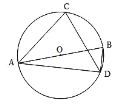
����Ŀ����ͼ�� AB ����O ��ֱ������ C �͵� D ����O �����㣬���� AC ��CD �� BD ���� CA= CD���� ACD = 80�� ������ CAB =______________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ѧУ���ڽ�ѧ¥����һ�����������г����һ�����ý�ѧ¥�ĺ�ǽ(�����õ�ǽ��Ϊ19 m)��������������ѧУ�����ܳ�38 m������Χ�ɣ�
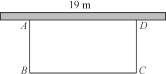
(1)��Χ�ɵ����Ϊ180 m2����������г�����ij��Ϳ���
(2)��Χ�����Ϊ200 m2�����г�����������ܣ����������Ʒ�,������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
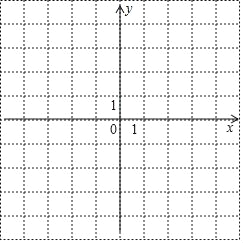
����Ŀ����֪һ�����κ���ͼ���ϲ��ֵ�ĺ�����![]() ��������
��������![]() �Ķ�Ӧֵ�����ʾ��
�Ķ�Ӧֵ�����ʾ��
| �� | ��3 | ��2 | ��1 | 0 | 1 | �� |
| �� | 0 | ��3 | ��4 | ��3 | 0 | �� |
(1)��������κ����ı���ʽ��
(2)�ڸ�����ƽ��ֱ������ϵ�л���������κ�����ͼ��
(3)��![]() ʱ��ֱ��д��
ʱ��ֱ��д��![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
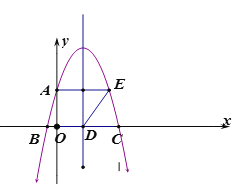
����Ŀ����֪:��ͼ������y=ax2+bx+![]() ��y�ύ�ڵ�A,��x�ύ�ڵ�B����C.����AB,��ABΪ��������ƽ���ı���ABDE,��E������������,��D����x����,�������ߵĶԳ���ǡ�þ�����D,�ҡ�ABD=60��,�����������ߵĽ���ʽΪ( )
��y�ύ�ڵ�A,��x�ύ�ڵ�B����C.����AB,��ABΪ��������ƽ���ı���ABDE,��E������������,��D����x����,�������ߵĶԳ���ǡ�þ�����D,�ҡ�ABD=60��,�����������ߵĽ���ʽΪ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ���ֱ֪��![]() ��������
��������![]() �ཻ�������ߵĶ���
�ཻ�������ߵĶ���![]() ����һ��
����һ��![]() ����
����![]() �ڵ������ޣ�
�ڵ������ޣ�
![]() ����
����![]() ����
����![]() �ĺ�����Ϊ
�ĺ�����Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
![]() ����
����![]() ��
��![]() ���ƽ������������
���ƽ������������![]() �ĶԳ��ύ�ڵ�
�ĶԳ��ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() ����
����![]() �����
�����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
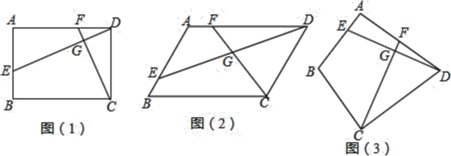
����Ŀ����֪�ı���ABCD�У�E��F�ֱ���AB��AD���ϵĵ㣬DE��CF���ڵ�G��
���ⷢ��
![]() ��ͼ
��ͼ![]() �����ı���ABCD�Ǿ��Σ���
�����ı���ABCD�Ǿ��Σ���![]() ��G��
��G��![]() ����գ�
����գ�![]() ______��
______��![]() ������ABCD��������ʱ��
������ABCD��������ʱ��![]() ______��
______��
��չ̽��
![]() ��ͼ
��ͼ![]() �����ı���ABCD��ƽ���ı��Σ���̽������
�����ı���ABCD��ƽ���ı��Σ���̽������![]() ��
��![]() ����ʲô��ϵʱ��
����ʲô��ϵʱ��![]() ��������֤����Ľ��ۣ�
��������֤����Ľ��ۣ�
�������
![]() ��ͼ
��ͼ![]() ����
����![]() ��G����ֱ��д��
��G����ֱ��д��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������y��ax2��4ax+4��a��0����y�ύ�ڵ�A��
��1�����A������������ߵĶԳ��
��2������B��0��3����y��Ĵ���l����������y��ax2��4ax+4��a��0����ֱ��l���������㣬�����п���y��Ľ���ĺ�����Ϊm����|m|��1����Ϻ�����ͼ����a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
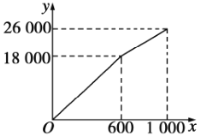
����Ŀ��Ϊ�ˡ������������У�������������������ij������Ͻ���ڵ�һ�����Ϊ![]() �Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ
�Ŀյؽ����̻���һ�����ֲݣ�ʣ�ಿ���Ի�.���ֲݲ��ֵ����Ϊ![]() ���ֲ��������
���ֲ��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ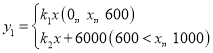 �������ͼ����ͼ��ʾ.�Ի��������
�������ͼ����ͼ��ʾ.�Ի��������![]() ��Ԫ����
��Ԫ����![]() �ĺ�����ϵʽΪ
�ĺ�����ϵʽΪ![]() .
.
��1�����![]() ��
��![]() ��ֵ��
��ֵ��
��2�����ֻ������С��![]() ʱ���̻��ܷ���Ϊ
ʱ���̻��ܷ���Ϊ![]() ��Ԫ����д��
��Ԫ����д��![]() ��
��![]() �ĺ�����ϵʽ��������̻��ܷ���
�ĺ�����ϵʽ��������̻��ܷ���![]() �����ֵ.
�����ֵ.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com