
分析 由当x=2时的函数值与x=6时的函数值相等可得二次函数图象的对称轴x=$\frac{2+6}{2}$,-$\frac{-2m}{2}$=4,据此可得m的值,从而得出函数解析式,继而即可求得x=8时的函数值.
解答 解:∵当x=2时的函数值与x=6时的函数值相等,
∴二次函数图象的对称轴x=-$\frac{-2m}{2}$=m=$\frac{2+6}{2}$,即m=4,
则二次函数的解析式为y=x2-8x-3,
∴当x=8时,y=64-64-3=-3,
故答案为:4,-3.
点评 本题主要考查二次函数图象上点的坐标特征,根据当x=2时的函数值与x=6时的函数值相等得出函数图象的对称轴是解题的关键.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:解答题
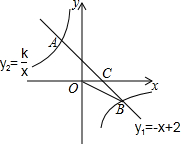 如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.
如图,一次函数y1=-x+2的图象与反比例函数y2=$\frac{k}{x}$的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4032×108 | B. | 4.032×1010 | C. | 4.032×1011 | D. | 4.032×1012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com