
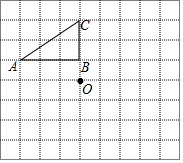
 如图,方格纸中每个小方格都是边长为1个单位长度的正方形,△ABC的顶点和点O均在网格图的格点上,将△ABC绕点O逆时针旋转90°,得到△A1B1C1.
如图,方格纸中每个小方格都是边长为1个单位长度的正方形,△ABC的顶点和点O均在网格图的格点上,将△ABC绕点O逆时针旋转90°,得到△A1B1C1.分析 (1)根据图形旋转的性质画出旋转后的△A1B1C1即可;
(2)过点O作OD⊥OA于点D,根据勾股定理求出OA的长,再由图形旋转的性质得出OA1=OA,OD⊥AA1,
由直角三角形的性质即可得出结论.
解答  解:(1)如图,△A1B1C1即为所求;
解:(1)如图,△A1B1C1即为所求;
(2)直线AA1是⊙O的切线.
过点O作OD⊥OA于点D,
∵OA=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
∴OA1=OA=$\sqrt{10}$,∠AOA1=90°,
∴AA1=$\sqrt{O{A}^{2}+O{A}_{1}^{2}}$=2$\sqrt{5}$.
∵OA1=OA,OD⊥AA1,
∴点D是OA1的中点,OD=$\frac{1}{2}$AA1=$\sqrt{5}$.
∵⊙O的半径为$\sqrt{5}$,
∴直线AA1是⊙O的切线.
点评 本题考查的是作图-旋转变换,熟知图形旋转不变性的性质是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
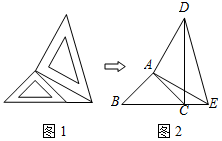 两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.
两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
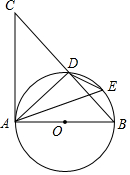 如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.
如图,以△ABC的边AB为直径作⊙O,交边BC于点D,点E是$\widehat{BD}$上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
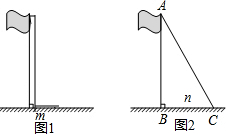 如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长m,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n,利用所学知识就能求出旗杆的长,若m=2,n=6,求旗杆AB的长.
如图,数学兴趣小组要测量旗杆的高度,同学们发现系在旗杆顶端的绳子垂到地面并多出一段(如图1),聪明的小红发现:先测出垂到地面的绳子长m,再将绳子拉直(如图2),测出绳子末端C到旗杆底部B的距离n,利用所学知识就能求出旗杆的长,若m=2,n=6,求旗杆AB的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com