
如图9,抛物线 与
与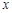 轴交于A、B两点,与
轴交于A、B两点,与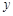 轴交于点C(0,
轴交于点C(0,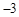 ).
).
(1)求抛物线的对称轴及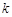 的值;
的值;
(2)抛物线的对称轴上存在一点P,使得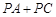 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.

解:(1)抛物线 的对称轴为:直线
的对称轴为:直线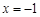 .…………(1分)
.…………(1分)
∵抛物线 过点C(0,
过点C(0,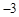 ),则
),则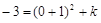 ,
,
∴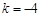 .…………(2分)
.…………(2分)
(2)如图9,
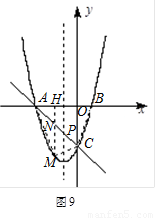
根据两点之间线段最短可知,当P点在线段AC上就可使 的值最小,
的值最小,
又因为P点要在对称轴上,所以P点应为线段AC与对称轴直线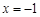 的交点.
的交点.
由(1)可知,抛物线的表达式为: .
.
令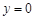 ,则
,则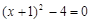 ,解得:
,解得: ,
,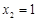 .
.
则点A、B的坐标分别是A(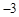 ,0)、B(
,0)、B(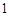 ,0).
,0).
设直线AC的表达式为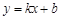 ,则
,则
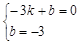 解得:
解得: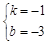
所以直线AC的表达式为 .…………(3分)
.…………(3分)
当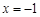 时,
时, 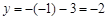 ,
,
所以,此时点P的坐标为(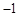 ,
,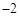 ). ………… (4分)
). ………… (4分)
(3)①依题意得:
当点M运动到抛物线的顶点时,△AMB的面积最大.
由抛物线表达式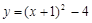 可知,抛物线的顶点坐标为(
可知,抛物线的顶点坐标为(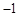 ,
,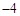 ).
).
∴点M的坐标为(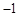 ,
,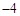 ). …………(5分)
). …………(5分)
△AMB的最大面积 . …………(6分)
. …………(6分)
②方法一:
如图9,过点M作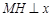 轴于点H,连结
轴于点H,连结 、
、 、
、 .
.
点M在抛物线上,且在第三象限,设点M的坐标为(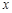 ,
,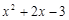 ),则
),则

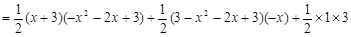
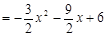 …………(7分)
…………(7分)
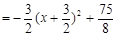 .
.
当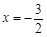 时,四边形AMCB的面积最大,最大面积为
时,四边形AMCB的面积最大,最大面积为 .………(8分)
.………(8分)
当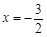 时,
时,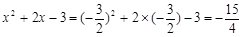 .
.
∴四边形AMCB的面积最大时,点M的坐标为(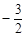 ,
,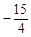 ). (9分)
). (9分)
方法二:
如图9,过点M作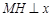 轴于点H,交直线AC于点N,连结
轴于点H,交直线AC于点N,连结 、
、 、
、 .
.
点M在抛物线上,且在第三象限,设点M的坐标为(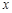 ,
,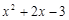 ),则
),则
点N的坐标为(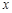 ,
, ),则
),则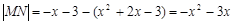 .
.
则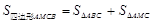
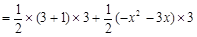
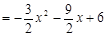 …………(7分)
…………(7分)
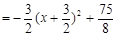 .
.
当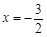 时,四边形AMCB的面积最大,最大面积为
时,四边形AMCB的面积最大,最大面积为 .………(8分)
.………(8分)
当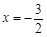 时,
时,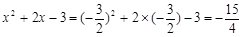 .
.
∴四边形AMCB的面积最大时,点M的坐标为(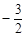 ,
,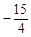 ). (9分)
). (9分)
【解析】略


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
如图9,抛物线与
轴交于A、B两点,与
轴交于点C(0,
).
(1)求抛物线的对称轴及的值;
(2)抛物线的对称轴上存在一点P,使得的值最小,求此时点P的坐标;
(3)点M是抛物线上的一动点,且在第三象限.
①当M点运动到何处时,△AMB的面积最大?求出△AMB的最大面积及此时点M的坐标;
②当M点运动到何处时,四边形AMCB的面积最大?求出四边形AMCB的最大面积及此时点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
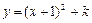 与
与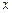 轴交于A、B两点,与
轴交于A、B两点,与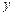 轴交于点C(0,
轴交于点C(0,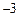 ).
).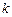 的值;
的值;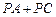 的值最小,求此时点P的坐标;
的值最小,求此时点P的坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
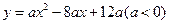 与
与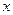 轴交于
轴交于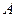 、
、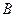 两点(点
两点(点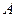 在点
在点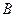 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点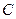 在第一象限,满足∠
在第一象限,满足∠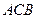 为直角,且恰使△
为直角,且恰使△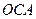 ∽△
∽△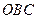 .
.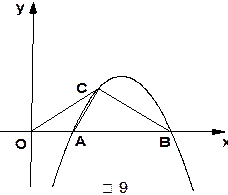
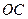 的长.
的长. 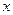 轴上是否存在点
轴上是否存在点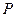 ,使△
,使△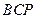 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的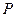 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源:2010-2011学年江苏省常州市考模拟数学卷 题型:解答题
如图9,抛物线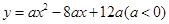 与
与 轴交于
轴交于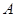 、
、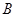 两点(点
两点(点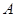 在点
在点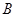 的左侧),抛物线上另有一点
的左侧),抛物线上另有一点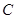 在第一象限,满足∠
在第一象限,满足∠ 为直角,且恰使△
为直角,且恰使△ ∽△
∽△ .
.
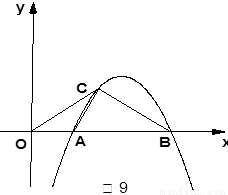
(1)(3分)求线段 的长.
的长.
(2)(3分)求该抛物线的函数关系式.
(3)(4分)在 轴上是否存在点
轴上是否存在点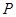 ,使△
,使△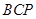 为等腰三角形?若存在,求出所有符合条件的
为等腰三角形?若存在,求出所有符合条件的 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com